0.9999... ≊ 1
What is infinity, and why it's not trivial to show that 0.9999... is equal to 1.
I’ve been long fascinated by the endless online debates about whether the infinite decimal expansion 0.9999… is exactly equal to 1. The canonical answer is yes. But there’s a considerable number of blogs and videos that will try to convince you otherwise — and in the process, expose the sinister machinations of Big Math.
What’s unique about this situation is that while it feels like bog-standard online crackpottery, it’s sort of running in reverse. The belief that 0.<whatever> must be less than 1.<whatever> makes perfect sense to rational people. Any website that tries to convince you otherwise probably also has some posts about chemtrails and reptilian mind control?…
The end result is that despite the existence of various proofs, the educators pretty consistently fail to impress this concept upon students — and it’s interesting to ponder why!
Proof stage 1: denial
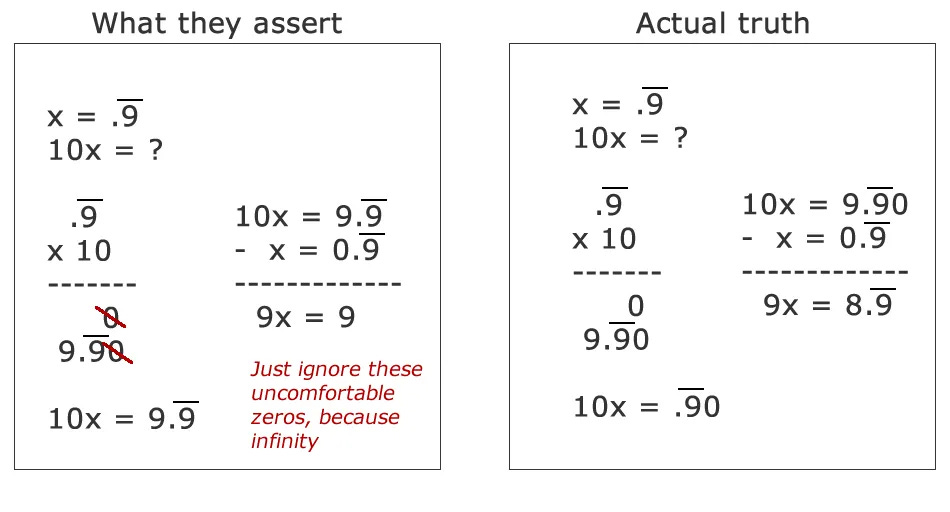
To get started, let’s consider the most common elementary sorta-proof:
It’s simple — but is it compelling? There are many questions one can ask. Is that endless decimal a faithful representation of ⅓, or are the dots covering up the fact that it’s always a bit off? Is it legal to multiply this infinite notation by a number? When multiplying a sequence of digits, aren’t we supposed to start at the infinitely distant right side — and how do we ever make it back from there?…
Of course, you can use intuition — but the whole point of this proof is to teach that intuition fails!
Fine. Let’s try another one:
Oh man, that’s even more suspect. We just multiplied an infinite decimal expansion by 10. Doesn’t that add a zero at the “end”? If not, where did the zero go?! A blogger exposes the shocking truth:
Some sources also give a proof by contradiction: if you have two different real numbers, you should be able to pinpoint a value in between. This is because there’s no such thing as minimal spacing between reals: any non-zero distance can be always divided into two. “So,” the proof-giver asks, “can you write a fraction halfway between 0.9999… and 1?” Some folks will accept the underlying premise and then conclude it’s not possible, but a witty student may “solve” the riddle the following way:
In the end, it’s not that these proofs are wrong, but if we’re playing fast and loose with infinity, we can just as easily “prove” that 0 = 1. We construct an endless sum of alternating +1 and -1 terms. Pairwise, the values work out to zero, so we can seemingly write the following equality:
But if the series has no end and we never run out of terms, isn’t it equally valid to shift the annotations one term to the right?
Now, it seems that the left side works out to one; it must be that 0 = 1.
The flaw in the proof is not that easy to articulate. Fundamentally, the issue is that we’re trying to think about infinity as a number — an odometer reading at the end of an infinitely long trip. Sure, we accept that the number is beyond our comprehension, but it still ought to be a number of some sort. The first equation hints that the number is even; the second suggests it’s odd. Can we categorically reject one of these choices? If not, then to circle back to the earlier proofs, how can we be sure about the numerical properties of endless decimals?
Proof stage 2: anger
To build a more rigorous explanation of why 0.9999… is equal to 1, we usually begin with a way to construct this fraction to n decimal places. A pretty self-evident method is the following sum:
The first term works out to 9/10 = 0.9, the second to 9/100 = 0.09, and so on. The resulting finite sum produces the number of nines specified by n.
To simplify the approach, we can rewrite each 9 in the numerator as 10 - 1. With this tweak, any m-th element of the sum can be restated this way:
Although that doesn’t seem like much of a simplification, plugging this into the original equation, we can see that all but the first and the last element now cancel out; for example, for n = 3, we get:
In other words, we can simplify the long sum to just the following:
After that, we hit a snag. We can’t just plug n = ∞ into the formula to figure out the value of 0.9999… to “infinity” digits. For one, as hinted earlier, there’s just no clear algebraic meaning to the symbol in the first place!
Granted, this can be a hard pill to swallow because we’re used to seeing notation such as this:
That said, in this use, “∞” is just a fancy calculator error message. It means “result out of range for reals”:
The symbol can’t be parsed as a number: instead of conveying information, it represents information loss. Again, recall the earlier troll proof that 0 = 1; we figured the pattern repeated some number of times, but we couldn’t decide if the number is even or odd. Heck, forget divisibility — is it even equal to itself? A thing is what it does; this thing doesn’t exhibit any of the useful properties of a number, so it can’t be treated as one.
The meaning of the symbol aside, there’s just no viable framework for the algebra of infinite or infinitesimal (infinitely small) values in the field of reals. To avoid complications, we allow real numbers to be arbitrarily big or small, but not infinitely big or small. Formally, they’re an Archimedean group. The axiom is roughly that if a and b are positive reals and a < b, there must exist some finite integer x that makes a · x > b. Infinite and infinitesimal quantities don’t obey that rule, so they’re not invited to the club.
So, how do we deal with this? Typically, instead of messing around with naked infinities, we are directed to use an analytic tool known as limits. In a nutshell, we examine what happens to the (1/10)n expression as n increases and try to infer where the sequence is ultimately headed. In this context, “infinity” is just process metaphor; we never actually do any arithmetic with infinite or infinitesimal values. Instead, we look at the road ahead and say “I don’t know how long this route might be, but it seems to be leading to <x>”.
Limits help us reason through tricky scenarios, such as the infinite + 1 - 1 case discussed earlier on (it endlessly oscillates between two distant values, so there’s no well-defined meaning to “sum at infinity”). That said, the case of (1/10)n is comparatively trivial. As n increases, the fraction gets vanishingly small but can’t conceivably cross into negatives, so the limit is:
Based on this analysis, we can assign a firm real-number meaning to (1/10)∞ and write:
Yet, to many folks, limits seem like a deficient foundation for the proof. The tool is mathematically sound but linguistically lousy: when we say that an expression “converges to <x> at infinity”, we don’t sound all that certain that the gap is ever fully closed. The more digits we look at, the smaller the difference between 0.9999… and 1 — but does it ever go down to zero, or does it just become infinitely small? Is Big Math pulling the wool over our eyes?!
Proof stage 3: bargaining
One way to trounce that argument is to reiterate that infinitesimals don’t exist in reals. In other words, one can treat the concept of limits with suspicion, but saying that 1 - 0.9999… is equal to “1/∞” makes about as much sense as saying that it’s equal to “√🐸”. Axiomatically, for real numbers, “infinitely close to 0” is the same as “0”.
Again, non-zero reals can be arbitrarily small but not infinitely small: per the Archimedean property, it must be possible to move them an arbitrary distance through integer multiplication. Infinitesimals don’t work that way. Loosely speaking, if we imagine “1/∞” as an actual number, there’s no finite integer we could multiply it by to get rid of infinity in the denominator.
In a moment of clarity, we could say that the equivalence between 0.9999… and 1 arises out of broken symmetry: we use a framework where numbers must be finite, but processes can continue without end. This is also what makes limits a valid mathematical tool, rather than just a vibe.
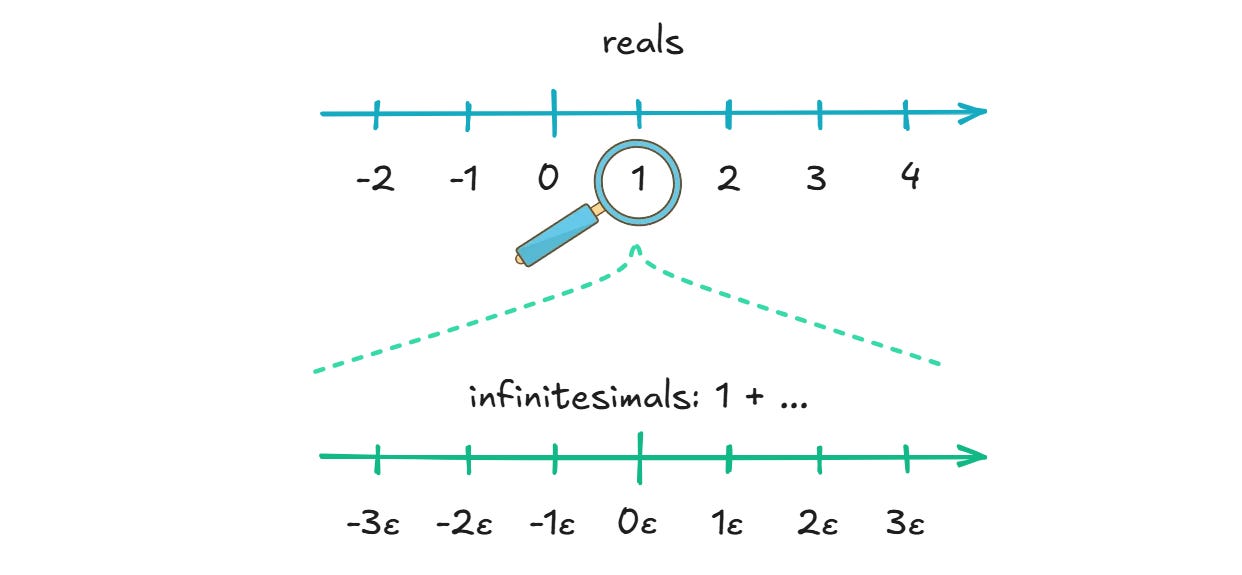
Of course, the explanation sounds a bit like a cop-out. The obvious rebuttal is “you’re just defining reals in a stupid way”. And you know what — that’s fair! Even if we can’t force Big Math to reconsider, we can point to the concept of hyperreals: a seemingly straightforward extension of reals that allows infinite and infinitesimal numbers to exist — and defines coherent algebra for both.
Within this system of “premium reals”, (1/10)n indeed nets an infinitesimal if n is an infinite number. So, it’s tempting to pick some infinite hyperinteger H and write the following:
At last, the truth comes out… right?
Proof stage 4: depression
Well, maybe! There’s an interesting nuance to this notation. And guess what — it once again boils down to the meaning of infinity.
To explain the issue in an accessible way, we can travel back to the kindergarten and recall the concept of counting numbers (1, 2, 3…). These numbers start from 1 and let us travel up the chain of magnitudes. Fast forward to elementary school: we get acquainted with the reciprocals of counting numbers (1, ½, ⅓…). This gives us a way to move down the same chain; using this new series, we can travel toward zero.
Conventionally, we say that the ultimate fate of this series is the same regardless of the value in the numerator: 1/n converges to zero just as 10/n would. That said, we can define a workable system where the information about the numerator is preserved “at infinity”, resulting in a universe of numbers that are infinitely close to zero but still differ from each other. Very loosely, we can imagine making a distinction between zero, “1/∞”, and “10/∞”.
These infinitesimal numbers are ordered and follow the usual rules of algebra within their own domain, but they’re smaller than any finite fraction can ever be. You can add an arbitrarily large infinitesimal to a real number and not register any movement on the real number line; this new realm can only be examined under a special mathematical microscope:
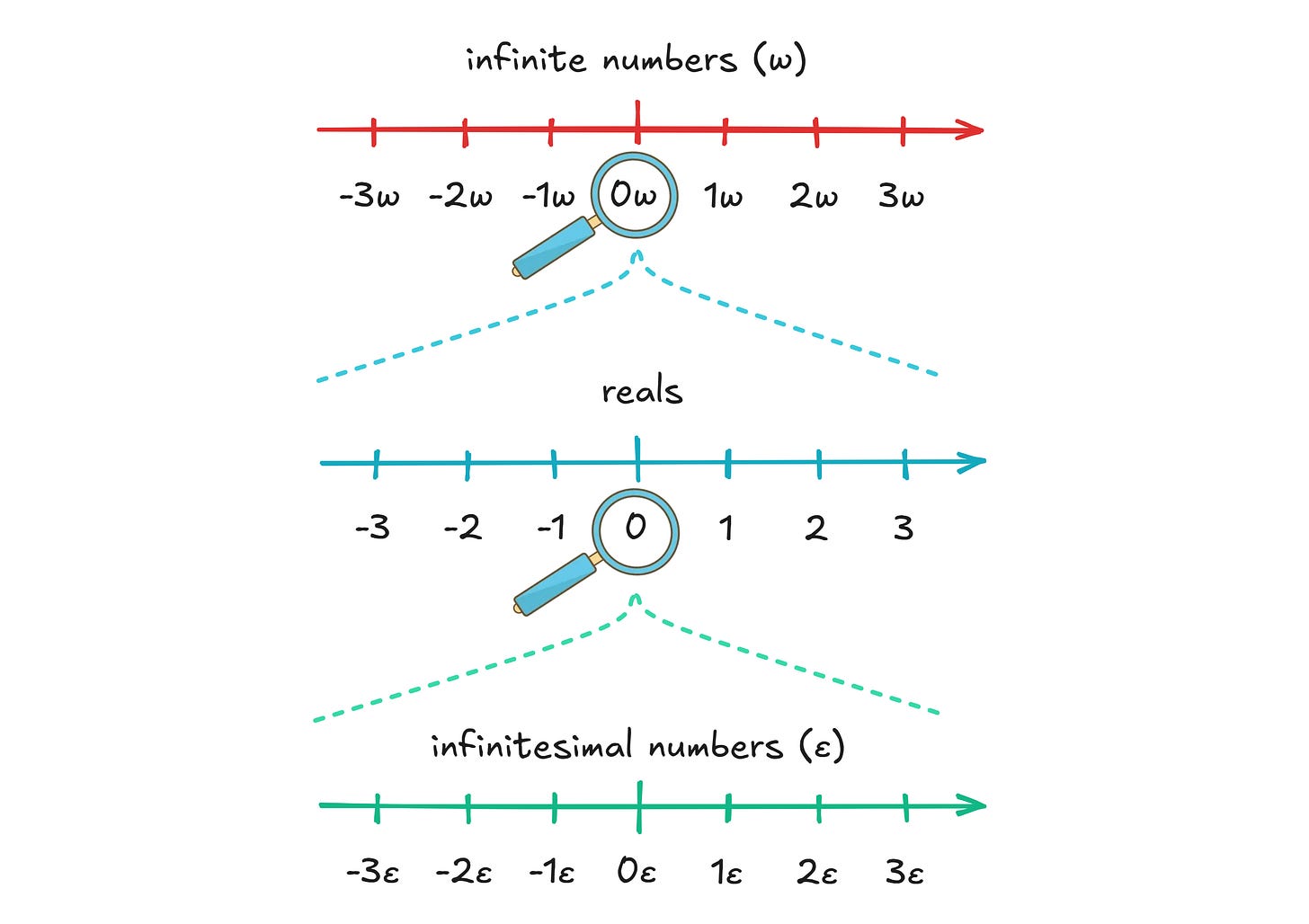
With these numbers in place, we can pull off the elementary school trick once more: we construct the realm of infinite numbers by taking a reciprocal (1/x) of the infinitesimals we introduced in the previous step. This adds a third number line “above” reals.
Infinite numbers structured this way are infinite in the sense of being larger than any real, but they are actual (or completed) infinities. They’re not a metaphor for looking at the road ahead; they represent specific, ordered odometer readings at the end of the trip. In particular, in an endless decimal, if we speak of a digit at a chosen infinite position H, the digit is clearly distinguished from the neighboring digits at H - 1 and H + 1.
This can be illustrated with a cute notation developed in the 1970s by Albert Harold Lightstone: use a semicolon to skip ahead in the decimal expansion, then add a hat symbol (sadly, ˆ and not 🎩) to pinpoint some infinite digit of interest. If we put the hat on the H-th digit, our earlier construction of the 0.9999… sequence can be written as:
Again, we’re saying that the pattern continues for H digits and then stops; we could cheekily call it a terminating infinite sequence. And yep, in this view, our earlier calculation checks out: 0.9999… and 1 differ by an infinitesimal amount.
That said, a cranky mathematician could come out of the woodwork and insist that “…” should mean that the nines continue forever after crossing H. In the Lightstone notation, we’d write this as:
This is what you could call a non-terminating infinite sequence.
If we accept this interpretation, we’re in a bit of a pickle. In essence, we’re dealing with a decimal expansion where the “number” of digits is somehow infinitely greater than any chosen infinite hyperinteger H. Our formula is no longer valid and we’re back to where we started in reals. We need to use limits or, I suppose, invent hyper-hyperreals.
Proof stage 5: acceptance
Which of these models is more correct? I don’t know! I don’t think that “…” has a definition that’s universal and precise enough to resolve the ambiguity. For every math buff who gets worked up about it, I’d wager there are ten who just shrug and say that “…” means “etcetera”.
It has to be said that if we pick the first option, some onlookers could accuse us of bias: the gods of mathematical abstraction offered us a way to express 0.9999… with more nines, yet we turned down their great gift. Are we taking the intellectual high road, or is it just that we want to see a specific result?
One thing is clear: we’re far from home. But if you wanted to, you could credibly argue that in “premium reals”, there is a difference between 0.9999… and 1. And then, internet strangers could get angry at you, demanding that you use the other interpretation of “…” or just generally stop horsing around.
Either way, it’s all in vain: the missing hyperreal “something” — which may be nothing — will always vanish when we return to the safety of plain, boring reals.
👉 For another view of infinite numbers, check out this article. Or, can I interest you in a proof that pi = 4 or in beaver math?
I write well-researched, original articles about geek culture, electronic circuit design, algorithms, and more. This day and age, it’s increasingly difficult to reach willing readers via social media and search. If you like the content, please subscribe!


Calling it the hyperreals always felt weird to me.
I prefer "reals 14 Max" or "reals 11 enterprise edition"
What you call "hyperreal analysis", I knew it as "non-standard analysis". This is to say, there is a difference between 0.999... and 1, but not in the real line. However, the argument stating that 10 x 0.999... = 9.999...90 is interesting. It's a Hilbert grand hotel where you accomodate the new guest 0.