A 15-minute intro to involute gears

Involute gears are everywhere: toys, kitchen appliances, cars. But what's so special about their shape?

In one of the earlier posts, I mentioned my perennial side hobby: CNC machining. In theory, it’s a straightforward and hassle-free way to make just about anything in the privacy of your home. In reality, it’s a portal to the demon-infested dimension of mechanical engineering and materials science. As with 3D printing, until you win that battle, you won’t have much luck making functional and durable parts.

One of the many rabbit holes I got pulled into over the years is the design of involute gears; I’ve written about this in depth elsewhere, but an accessible intro might save some readers a lot of time.

Of course, gears seem obvious — but trying to eyeball the shape always ends in tears. The correct solution has a couple of remarkable properties: properly-designed gears roll with little friction or vibration, turn at a constant speed, and transfer torque without any discontinuities or snags.

A close-up of two meshing involute gears.

On the internet, there’s no shortage of mathematical formulas you can reuse, and there are tools that let you generate the requisite shapes for use with your favorite CAD tool. Still, it can be interesting to derive the geometry from first principles; if nothing else, the knowledge lets you crank out exotic (e.g., non-circular) gears with ease.

Walking in a straight line

We can start with the degenerate case of a rack — i.e., a straight bar (or, more obtusely, a small section of an infinite-diameter gear). If we want to transfer linear motion from one such bar to another while still maintaining the ability to separate the components down the line, the most obvious solution is to cut an array of symmetric, rectangular slots into the edge of each bar:

A pair of rudimentary racks.

The benefit of straight teeth over angled profiles is that there’s no force pushing the racks apart, and thus no risk of slippage. That said, the solution is suboptimal in other respects. For one, every tooth is essentially a small lever — so especially if there’s any flexing or misalignment, we’re bound to see a concentration of mechanical stress at the base. We can make the mechanism a lot stronger without adding any bulk if we tilt the side walls:

Racks with angled teeth.

Again, the trade-off is that the force vector between the meshing surfaces is now angled; if there’s not enough friction and too much play in the assembly, the gears could pull apart and slip. In fact, if we crank the angle all the way up — to 90° from vertical — we end up with two smooth surfaces touching at the centerline!

Silly extremes aside, pressure angles between 15° and 25° from vertical are considered optimal in most cases; lower angles are favored for precision assemblies because they tend to have less backlash even if not aligned perfectly; higher values produce beefier teeth for ultra-heavy loads.

Real gears have curves

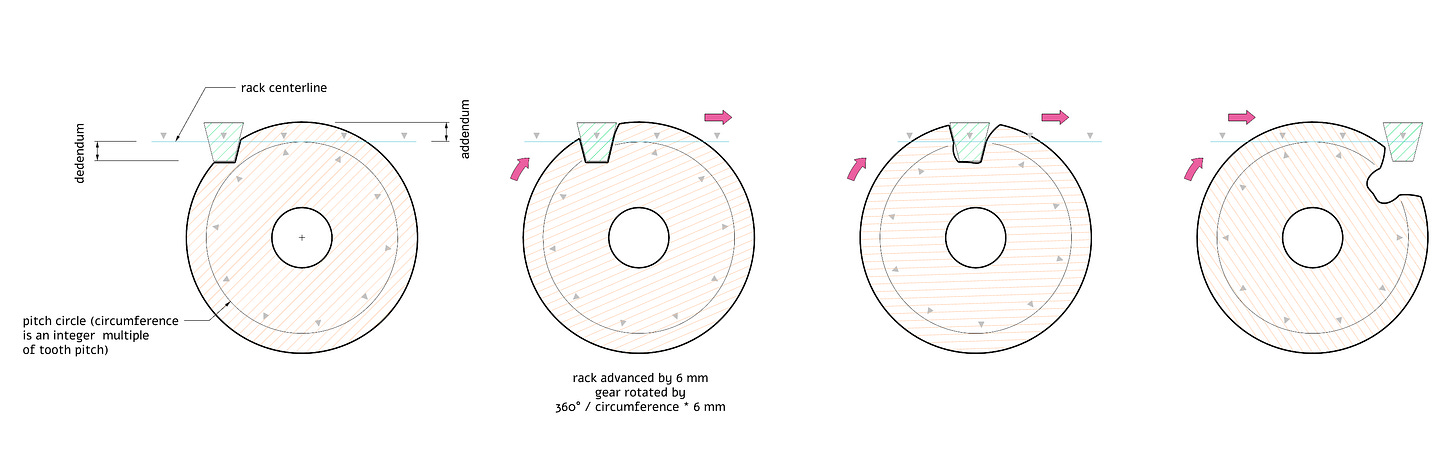
If we have a circular gear meshing with a rack, we want them to move without slippage. In other words, every time the rack advances some linear distance, the gear ought to roll exactly that far along some fundamental circumference C (the pitch circle). From basic geometry, linear rack travel of n should translate to circle rotation of θ = 360° / C * n.

Further, for continuous rotation, the circumference of the pitch circle needs to be an integer multiple of tooth pitch. This term stands for the length of the entire tooth pattern — not just the protruding part, but also the matching negative clearance that follows. (If you need a visual, see the annotations on the image above.)

With the pitch circle drawn for the desired tooth count m, and then some addendum tacked on to match the depth of the rack (customarily: tooth pitch / π), we can simulate the meshing process — treating the rack as a virtual cutting tool that progressively removes material from the gear:

The involute gear cutting process (m = 10).

Again, as noted earlier: every time the rack moves forward, the gear rolls along the pitch circle by the same amount.

The cutting process produces a geometry with single, tangent contact for every position of the rack tooth — ensuring consistent direction of the force vector and a constant speed.

Further, the resulting shape can mesh not only with the rack that generated it, but with any other gears that share the same pressure angle, tooth pitch, and tooth height. To understand why, imagine squeezing an imaginary, double-sided rack in between the two gears:

Two round gears meshing via an imaginary rack.

By design, each gear is made to mesh with the rack along a straight path dictated by the pressure angle; it follows that they mesh with each other, too.

Another way to look at the cutting process is to view it from the perspective of an observer stationed on the rotating gear:

Rotating gear POV.

From this perspective, the cutting tooth enters at an angle before righting itself — and then tilts in the other direction as it’s camming out. Its horizontal wall leaves behind a rounded involute curve near the top; the bottom edge often produces a low-lying undercut on the opposite side.

The involute curve is what makes the gear tick; the undercut is undesirable, as it weakens the part (and in extreme cases, can severely compromise the involute). The undercutting behavior, neglected in many gear-making tutorials, is more pronounced at lower tooth counts. Undercuts are also more prominent at lower pressure angles, as shown below:

The effect of pressure angle on undercuts for small gears.

On the flip side, gears with high pressure angles are not only more prone to backlash, but can be trickier to manufacture due to diminished clearance at the bottom of the machined profile. Luckily, there is a way to make low-tooth-count gears without jacking up pressure angles: we can shift the cutting profile.

To make a profile-shifted gear, we move the cutting teeth up in relation to the rack’s centerline; the addendum on the gear is adjusted correspondingly, too:

Profile-shifted gears, compared to the vanilla geometry.

The modified gear is more robust, but it can only mesh with gears that have a complementary (opposite) profile shift. This makes the trick useful only if the mating gear has a comparatively high tooth count. If both gears are small, we’re strengthening one of them, but ruining the other with an inverse profile shift that makes its undercuts much worse.

There’s a lot more to gear science — but the constructive method outlined above makes the rest easy to explore. For example, if you trade the pitch circle for a freeform curve, you can make some impractical (but working) Dalí-esque gears for much-deserved YouTube views.

---

I write well-researched, original articles about geek culture, electronic circuit design, algorithms, and more. This day and age, it’s increasingly difficult to reach willing readers via social media and search. If you like the content, please subscribe!