Complex numbers #2: a world in 3D
Why is there no equivalent of complex numbers for three dimensions? And what's the deal with quaternions?
Several days ago, I posted a brief introduction to complex numbers. My goal was to explain the concept better than usual; I wanted to show that the imaginary unit of i = √-1 is not just a whimsical separator between two unrelated variables. Instead, it encodes a deliberate and important relationship between the real and imaginary part.
The reason many sources don’t pay attention to this detail probably has to do with the name; “imaginary” implies that √-1 is just some sort of an in-joke. To be fair, early mathematicians — who came across imaginary numbers in the context of solutions to polynomial equations — thought of them as paradoxical or useless. That said, formalizations of mathematics have come a long way. Today, there’s nothing “real” about reals to begin with; most of them aren’t even computable! Conversely, imaginary numbers aren’t second-class citizens. If you have a set of tokens and can define a coherent algebra over it, you’re in the game.
For complex numbers, the novel algebra boils down to a simple table that specifies what happens to the imaginary unit during multiplication:
In today’s article, I’d like to address two additional questions about this design: first, can we extend this to three dimensions; and second, what the unholy heck are quaternions?
The problem with z
In the previous article, we established that, if you represent a pair of Cartesian coordinates as a complex number (v = x + iy), then multiplying this number by im will rotate it by m · 90°. Together with more obvious methods for translation and scaling, this means that complex numbers serve as a powerful model for two-dimensional geometry.
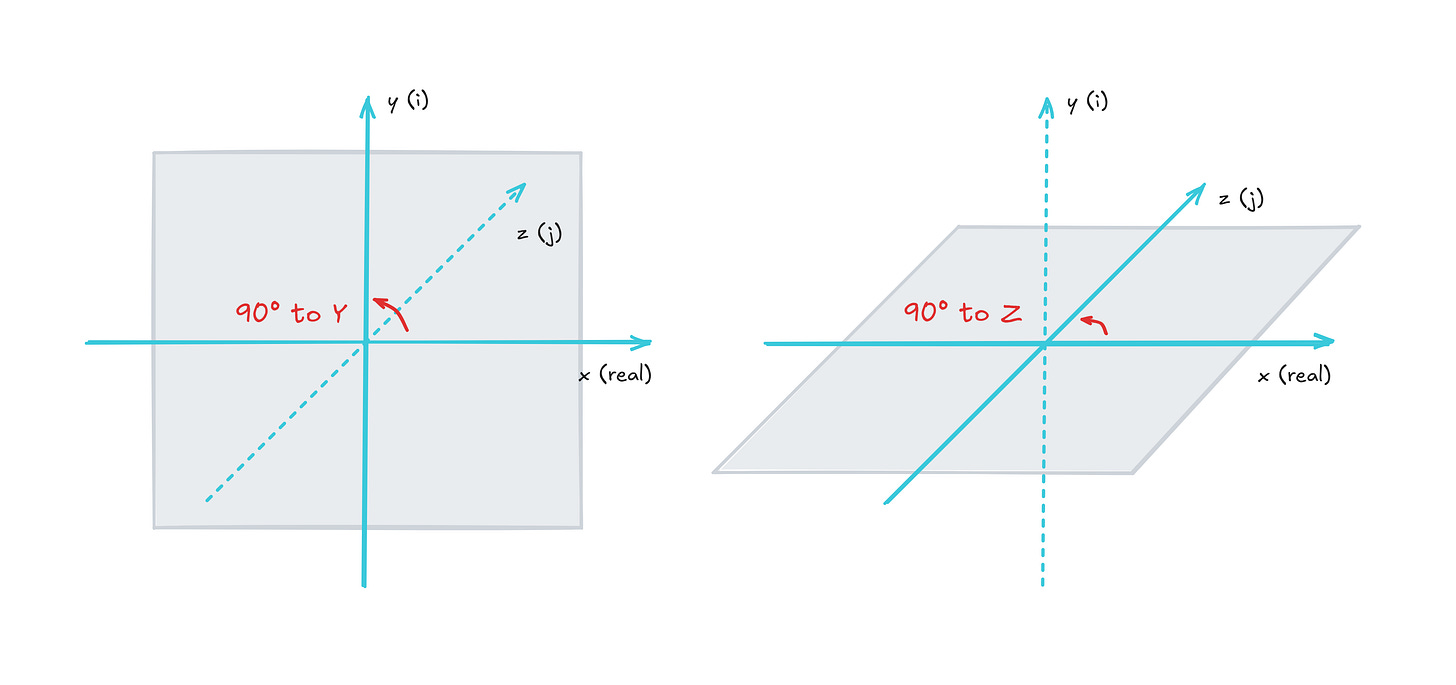
Points in three dimensions are typically represented by three Cartesian coordinates: x, y, and z. At first blush, we should be able to extend complex numbers to also incorporate z. It seems that all we need is another imaginary unit, j, with multiplication rules that can be figured out at a later date:
Alas, this is a dead end. In two dimensions, we have just one fundamental mode of rotation, corresponding to motion in the XY plane. In 3D, we have three fundamental modes — one in the XY plane, one in XZ, and one in YZ:
We can define the algebra for our imaginary units so that multiplication by a power of i spins a point in the XY plane, and then make it so that multiplication by a power of j results in rotation in the XZ plane — but we run out of options for YZ.
Enter the quaternion
The 19th century half-solution is to add a fourth imaginary unit, k. This results in a four-dimensional “hypercomplex” number that can represent a point in 4D space. We can use this space solely for three-dimensional shapes, but we do need that extra degree of freedom to have a full set of rotations baked into simple algebra.
We’re going to do the sensible thing and label the coordinates of the 4D space as x, y, z, and 🌀. With this sorted out, we construct the quaternion:
Next, let’s try to define the algebra for this thing — that is, let’s build a complete multiplication table for the imaginary units:
To preserve the ability to scale objects and to maintain general sanity, we start by specifying normal rules for multiplication by 1:
To proceed past that point, we need to make an important observation: in any sensible (i.e., Euclidean) geometry, all axes are orthogonal. This means that no matter which axis you’re on, there’s always a single 90° rotation that gets you to any other axis of your choice.
As an obvious demonstration, in three dimensions, we can always from x to y or z in single 90° step:
The same goes for moving from y to x or z, and from z to y or x.
Although we don’t have the faculties to imagine orthogonality in four dimensions, this principle means that the y, z, and 🌀 axes, when considered in isolation, all have functionally the same relationship to the real axis (x). Any observation we make for the XY plane is also going to generalize in a straightforward way to the XZ plane and the X🌀 plane.
With 2D complex numbers, if we have some scalar value a on the real axis and want to repeatedly rotate it by 90° in the XY plane, we keep multiplying it by i:
In other words, we’re cycling through the following progression of multipliers for the starting number a:
If a = 1, we can restate this as:
This describes rotation in the XY plane. Again, because the y axis, the z axis, and the🌀 axis are all orthogonal to x, an analogous rotation patterns out of and into the x axis also hold for the XZ plane (1 · j = j, j · j = -1 …) and the X🌀plane (1 · k = k, k · k = -1…).
This allows us to fill in a bunch of additional fields in the multiplication table:
This is as far as we can get while staying tethered to the safety of the x axis. Next, let’s hop into the three-dimensional XYZ space.
Straight outta flatland
Once again, there are three fundamental rotations of interest in the XYZ space. That said, we already have definitions for rotations in the XY and XZ plane, so the only mystery is the YZ case:
To model this, we can start with a positive value on the horizontal, j-coupled z axis. We’re turning counter-clockwise toward the vertical, i-coupled y axis. It follows that we can expect the following progression of multipliers for the scalar value:
As before, we want this progression of values to arise from repeated multiplication by one of the three imaginary units (i, j, or k) — but in contrast to the earlier x axis scenarios, it’s not immediately obvious which one.
There’s no need to overthink it: only one answer fits! We’ve established earlier on that j · j must be equal to -1, so there’s no way that multiplication by j could get us from value #1 (j) to value #2 (i) in the aforementioned chain. Similarly, we know that i · i = -1, so multiplication by i can’t possibly get us from value #2 (i) to value #3 (-j). The only remaining option is that rotation in the YZ plane must be the consequence of multiplying j or i by k:
This gives us two more data points for the multiplication table:
Feels like we’re on a roll… but at this point, we’re actually out of options to figure out the rest in the XYZ space.
Engage the hyperdrive!
For the next trick, recall that y, z, and 🌀 are all orthogonal to x. We have previously used this to equate the XY plane to XZ and X🌀 — but in the same vein, a 3D slice that contains the XYZ space is not really different from a slice that contains the XZ🌀 space:
We don’t need to visualize a rotation that gets us from XYZ to XZ🌀; it’s enough to know that it must be possible because of orthogonality.
The gotcha with any such deus ex machina rotations is that we need to be careful not to mix up the directions of the axes, as that would mess up the signs in the multiplication table. This is why I’m keeping x firmly in place and I’m cycling through an orderly progression of y → z → 🌀 for the other two dimensions.
In any case, in the XZ🌀 frame of reference, we can do precisely what we did for the XYZ case just moments before. We take a look at where the YZ plane used to be (now: Z🌀). We pick a point on the horizontal, k-coupled 🌀 axis and rotate it toward the j-coupled z axis. The only viable, paradox-free multiplier for this is i:
This nets more blood for the blood god entries for the multiplication matrix:
The final step is spinning the dial once again to move from the XZ🌀 space to X🌀Y. Again, we’re keeping the x axis fixed and just cycling through a sequence of y → z → 🌀 for the other two axes:
There are no surprises in this view; we can once again focus on where the YZ plane used to be (now: 🌀Y). Rotating an point on the i-coupled y axis onto the k-coupled 🌀 axis reveals the following rules:
Plugging that into the multiplication table, we finally reach the finish line:
Congratulations, it’s quaternions!
But here’s the bad news: the algebra for quaternions is non-commutative — or, as scientists say, “real messed up”. Note, for example, that k · i ≠ i · k.
This doesn’t invalidate the result, but it makes quaternions even less intuitive than the presence of four dimensions would imply. The same problem crops up for higher-dimensional complex numbers constructed in this fashion, no matter how much we try.
You can go through life without ever encountering quaternion algebra, but it crops up in some niches related to 3D graphics and robotics. There’s just one real reason for it: in the quaternion space, there is a simple and easily-memorized formula for rotating a point by an angle around a line of our choice. To arrive at that neat formula, you need to stuff the 3D object into the higher YZ🌀 space (i, j, k) instead of XYZ (1, i, j). To be clear, the same rotation logic can be written for separate (x, y, z) coordinates — but this expanded form is long-winded, impossible to remember, and no one wants to deal with it when it’s time to write some code.






Not bad! I'm a little surprised you didn't mention Hamilton's famous equation: i²=j²=k²=ijk=-1.
FWIW, there's an easy way to remember the multiplication rules: i ⇔ j ⇔ k ⇔ i (best represented by a three-part circle combining the two instances of i). When you go right-to-left (or clockwise around the circle) the result is positive. When you go left-to-right (or counterclockwise), the result is negative.
So, j×k=+i but k×j=-i.
BTW: On my browser, the spiral symbol you used for the 4D axis just shows as a box; the browser doesn't support it. I looked in the app, and it appears okay there. For some authors, the canonical 4D axis is w (and the 5D axis is u), which is an easier typography. I think of them as standing for Weird and Unusual. For more than five dimensions, I've seen authors use xₙ, usually starting at x₁.
Are you next going to enter the deeper waters of octonions? 😁
> There’s just one real reason for it: in the quaternion space, there is an easily-memorized formula for rotating a point by an angle around a line of our choice.
Isn't the primary reason not the ease of the formula, but to avoid gimbal lock? Euler angles are a lot more intuitive for people otherwise. (I suppose there are also some computational benefits but I don't think that was the primary driver historically?)