A 20-minute intro to complex numbers

You might have heard of complex numbers before -- but what's the actual significance of i = √-1?

In a couple of earlier articles on this site, I brought up complex numbers. They are a fairly abstract construct that reeks of higher math, but that is hard to avoid in the context of analog electronics, signal processing, computer graphics, and more.

If you’re a subscriber, you may already have an inkling of how complex numbers work; the mechanics are explained in many places on the internet and are probably required for CS and EE degrees. That said, accessible texts usually don’t explain what’s cool about this construct — and in particular, why it’s uniquely suited as a model of two-dimensional Cartesian geometry, phase-shifted electronic signals, and other “orthogonal” quantities.

The cat coordinate system

The most basic (if somewhat flawed) way to introduce complex numbers is to say that they’re a trick to express two independent, real numbers as a single variable while keeping the two halves at an arm’s length. This is done by coupling one of the numbers to a magic-bean value of i:

\(z = x + iy\)

We call the free term (x) the “real” part, and the i-coupled term (y) the “imaginary” part.

A more accessible way to put it would be to say that we invented a value of 🐱, with the rule that 🐱 is not a normal number. There are no obvious arithmetic rules that would allow you to combine the terms that contain a 🐱 with the ones that do not, but you’re free to work on each part separately.

Addition and subtraction can be pretty intuitively extended to cat-complex numbers by individually summing the cat-free and cat-bearing parts:

\(\underbrace{(3 + 2🐱)}_{\substack{\textrm{cat-complex} \\ \textrm{number 1}}} + \underbrace{(1 + 5🐱)}_{\substack{\textrm{cat-complex} \\ \textrm{number 2}}} = \underbrace{\underbrace{(3+1)\vphantom{🐱}}_{\textrm{non-cat count}} + \underbrace{(2+5)\vphantom{🐱}}_\textrm{cat count}🐱}_\textrm{cat-complex result}\)

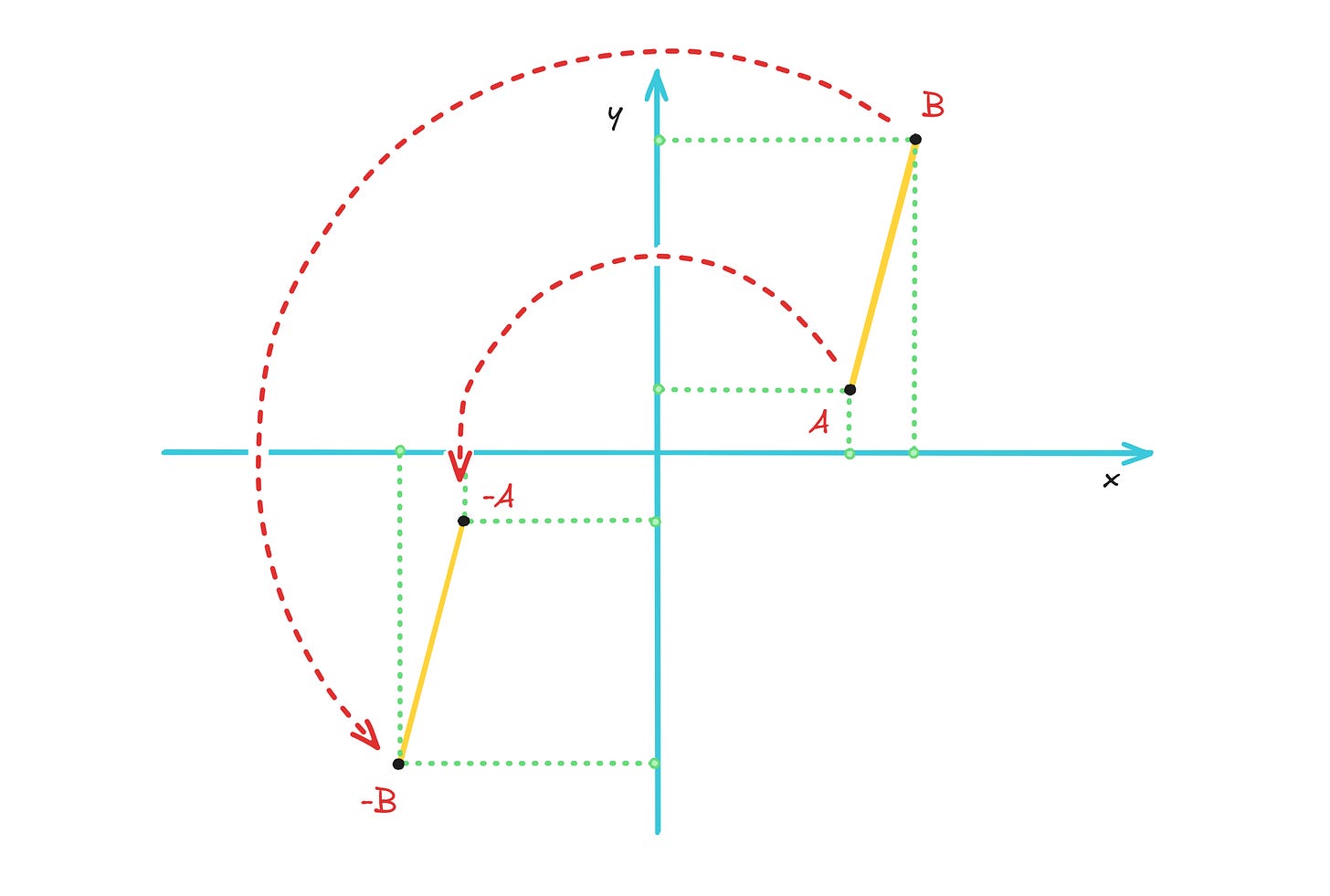
This aligns with intuition about the real world; for example, if the cat-free part represents horizontal distance and the cat part represents elevation gain, summing the corresponding cat-complex numbers for different segments of a mountain trail can give us the totals for the hike:

Adding hike segments in cat-space.

In a boring math paper, they would make you delete the cats and use i instead, but the semantics of addition and subtraction remain the same:

\(\underbrace{(x_1 + iy_1)}_{z_1} + \underbrace{(x_2 + iy_2)}_{z_2} = \underbrace{\underbrace{(x_1 + x_2)}_\textrm{real part} + i \underbrace{(y_1 + y_2)}_\textrm{imaginary part}}_{\textrm{complex result: } z_1 + z_2}\)

The rules for multiplication by real numbers follow from addition and are similarly obvious. You multiply the real and imaginary parts independently:

\(a \cdot \underbrace{(x + iy)}_{z} = \underbrace{\underbrace{(a \cdot x)}_\textrm{real} + i \underbrace{(a \cdot y)}_\textrm{imaginary}}_{\textrm{complex result: } a \cdot z}\)

If we’re using complex numbers to represent (x, y) points on a Cartesian plane, then addition moves them by some specified distance, while multiplication by a positive value scales the geometry in relation to the center of the coordinate system.

Making the cat spin

We could stop there: a system that uses 🐱 or that defines i as an abstract symbol works just fine. That said, for geometry, it’s just not a big improvement over keeping track of x and y coordinates as separate entities and manipulating them individually. The cat symbol is cool, but it doesn’t offer any special insights into reality.

The core problem is that the cat-based model doesn’t encode any specific relationship between the two values. As far as it’s concerned, the cat domain and the non-cat domain are completely disjoint. They are two different number lines on two separate sheets of paper.

These are not the mechanics of the two-dimensional Cartesian coordinate system: the axes are orthogonal. They are mostly separate, but we expect there to be a rotation operator that transposes one axis onto another. Alas, in our 🐱-coupled system, rotation is not intrinsically defined.

OK, I lied: we have the notion of rotating a point by 180°. It’s equivalent to scalar multiplication by -1:

\(-1 \cdot (x + iy) = \underbrace{(-x)}_\textrm{real} + i \underbrace{(-y)}_\textrm{imaginary}\)

The operation flips the signs of both coordinates. For a pair of points on a plane, we’d get the following result:

Wheeeeee!

Upon closer inspection, we can intuit that it’s not the magnitude of the scalar value (-1) that’s doing the hard work; if we switch to -2 or -0.5, the objects change scale, but they’re still rotated just 180°.

Instead, a full turn (360°) requires multiplying by -1 twice. Continuing down that path, multiplying by -1 three times in a row results in a 540° turn (180° · 3), and so on. In other words, the secret sauce appears to be the exponent of a constant -1 base:

\(\begin{align} z \cdot (-1)^0 &\rightarrow 0^\circ \\ z \cdot (-1)^1 &\rightarrow 180^\circ \\ z \cdot (-1)^2 &\rightarrow 360^\circ \\ z \cdot (-1)^3 &\rightarrow 540^\circ \\ z \cdot (-1)^4 &\rightarrow 720^\circ \\ ... \\ z \cdot (-1)^m &\rightarrow 180^\circ \cdot m \\ \end{align}\)

So, what would it take to achieve rotation by 90°? Well, looking at the series above, the answer seems pretty clear, if weird. We need to choose an exponent of ½:

\(z \cdot (-1)^{½} \rightarrow 180^\circ \cdot ½ = 90^\circ \\\)

In the Cartesian view of complex numbers, if we take a real value and attach it to i, we’re essentially saying that it no longer represents a distance on the x axis, and instead represents the same distance on the y axis. That’s rotation by 90°. It follows that to automatically encode orthogonality between the two parts of a complex number, we ought to define i as (-1)^½.

But what’s (-1)^½?

If you had any prior exposure to complex numbers, you already know the “official” answer, but it can be useful to ponder how we arrive at that. Let’s start with the basic, middle-school definition of positive integer powers. It’s a convenient notation that replaces repeated multiplication:

\(n^a = \underbrace{n \cdot n \cdot n ...}_{\textrm{repeats } \times \ a}\)

We have no real-world intuition about what it means to raise n to anything other than a positive integer, but it suffices to make another obvious observation about the equivalence of n^a · n^b and n^{a + b}:

\(n^{a}\cdot n^{b} = \underbrace{\underbrace{n \cdot n \cdot n ...}_{\textrm{repeats } \times \ a} \cdot \underbrace{n \cdot n...}_{\textrm{repeats } \times \ b}}_{\textrm{repeats } \times \ a + b} = n^{a+b}\)

This equality gives us a lead for n⁰:

\(n^a = n^{a+0} = n^a \cdot \underbrace{n^0}_{= \ ?} \)

The only possible multiplier for n^a that produces n^a is 1, so in an internally-consistent algebra system, that must be the value of n⁰. Roughly the same logic can be used to figure out the meaning of n^-a:

\(\begin{array}{c} n^{a-a} = n^0 = 1 \\ n^{a-a} = n^{a+(-a)} = \underbrace{n^a \cdot \underbrace{n^{-a}}_{= \ ?}}_\textrm{must be 1} \end{array}\)

The first half of the expression — n^a — expands to a product of a repetitions of n. The only way to get back to 1 is for n^-a to be the reciprocal of n^a — that is, to expand to a repetitions of 1/n.

This brings us to simple fractions. Whatever the meaning of n^½ might be, we want the following to hold:

\(n = n^1 = n^{½ \ + \ ½} = \underbrace{n^½}_{ =\ ?} \cdot \underbrace{n^½}_{ =\ ?}\)

Exponentiation has two inverse operations: roots (mapping result & exponent → base) and logarithms (mapping result & base → exponent). In this instance, since we’re looking for a value that gives us n when squared, we need the square root of n; in other words, n^½ = √n.

Tying it all together

At this point, we can more conventionally describe the value we’ve been looking for: i = (-1)^½ = √-1.

The value of i is not real (in the sense that it doesn’t have a place on the ℝ number line), so it obeys the design rule of the 🐱-based system: it keeps the orthogonal coordinates separate. The exception is that multiplication of a complex number by i^m results in a rotation of m · 90°. For example, for m = 1, we can see that the x and y coordinates change places:

\((x + iy) \cdot i = (ix) + (\underbrace{i \cdot i}_{= \ -1} \cdot y) = \underbrace{(-y)}_\textrm{real} + i \underbrace{(x)}_\textrm{imag}\)

We’ll get to the way to deal with fractional m values in a moment.

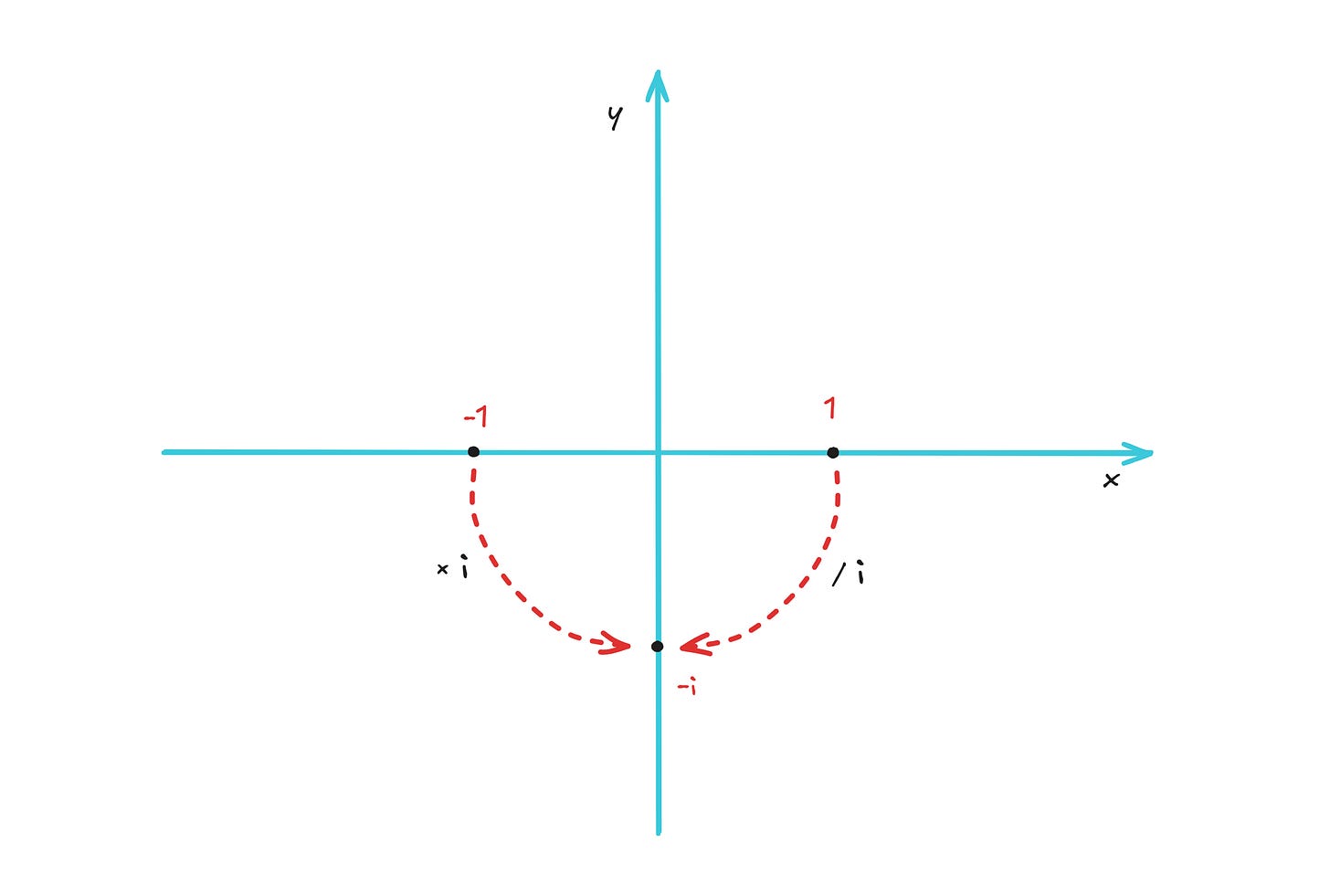
For the most part, rudimentary complex number algebra is straightforward, but there are some surprises. We have previously established that multiplying by i twice just flips the sign of the starting number: z · i² = -z. If we divide both sides of this equation by i, we get z · i = -z / i. After further simplification, we arrive at a peculiar but unavoidable corollary: i = -1/i, which can be also written as -i = 1/i.

There is a geometric explanation of this result, too! If multiplying by i is equivalent to a rotation by 90°, then to get us back to the starting point, division by i must correspond to rotation by -90°. It follows that in the geometric view, taking -1 on the real axis and rotating it by +90° (-1·i, aka -i) ought to produce the same result as taking +1 and rotating it -90° (1/i):

Division and multiplication in the complex plane.

To build a more general model of complex multiplication, we can note that any point on a two-dimensional plane that’s described by its (x, y) coordinates can be also unambiguously described by its distance from (0, 0) and an angle:

Two ways of saying the same thing.

This representation is known as polar coordinates. The technique is fairly common in computer graphics and engineering; there are simple trigonometric conversions between the two. When applied to the complex plane, the trick allows us to imagine any complex number as a real value l on the x axis that’s rotated by some angle m · 90°. Based on what we discussed earlier, we already have a formula to do this exact thing:

\(z = l \cdot i^m\)

The length l is usually referred to as the modulus or the absolute value. The angle (again, m · 90°) is called the argument, apparently as an homage to an astronomical term that dates back to the 14th century.

This notation is surprisingly useful. For example, the polar form gives us a neat geometric interpretation of what it means to multiply two complex numbers. If we represent each number using the polar formula, we get:

\(\underbrace{(l_1 \cdot i^{m_1})}_{z_1} \ \cdot \ \underbrace{(l_2 \cdot i^{m_2})}_{z_2} = (l_1 \cdot l_2) \cdot (i^{m_1} \cdot i^{m_2}) = \underbrace{(l_1 \cdot l_2) }_{\textrm{new } l} \ \cdot \ i^{\overbrace{ {m_1 + m_2}}^{\substack{\textrm{new m}}}} \)

In essence, the result is that the lengths are multiplied while the angles add.

The multiplication formula, in turn, gives us an explanation of a certain method to get rid of complex numbers in the denominator of a fraction. Such denominators can be annoying to work with, and in textbooks, you’re instructed to multiply both the numerator and the denominator of the troublesome fraction by what’s known as the complex conjugate. In plain English: if the denominator is z = x + iy, the complex conjugate is just a version of z that has the sign of the imaginary part flipped: z^* = x - iy.

The result is always a real-only denominator — but how did we come up with this and why does it work? The simplest answer is to imagine a plot of both z and z^*. On a Cartesian plane, they’re essentially the same, except the y coordinate of z^* is flipped, producing a mirror image in respect to the horizontal axis. This means that in the polar-coordinate representation, the lengths of z and z^* are the same (l₁ = l₂), while the angles have the opposite sign (m₁ = -m₂). If we use the earlier formula to calculate the product of z · z^*, it follows that the angles net out to zero (i.e., the new nominator is real-only) while the new l is equal to the square of the starting length.

Another neat use of the polar notation has to do with the fact that rotations in two dimensions can also be described with basic trigonometry. When working with separate x and y coordinates, we’d use the following formula to rotate a point on the x axis by some chosen angle α:

\(\begin{align} x_{rotated} = x_{orig} \cdot cos(\alpha) \\ y_{rotated} = x_{orig} \cdot sin(\alpha) \end{align}\)

This gives us a yet another to represent complex numbers: as a scalar length l (again, that’s the modulus) multiplied by the cosine of an angle α to construct the real part, and the sine coupled to i to construct the imaginary part:

\(z = l \cdot [cos(\alpha) + i \cdot sin(\alpha)]\)

This might seem mundane, but combining the new formula with the earlier polar representation (z = l · i^m), we can write the following identity:

\(\underbrace{l \cdot i^m}_{\substack{\text{rotation} \\ \text{method 1}}} = \underbrace{l \cdot [cos(m \cdot 90^\circ) + i \cdot sin(m \cdot 90^\circ)]}_{\substack{\text{rotation method 2}}}\)

If we substitute l = 1 and switch to radians, we get a equation that allows us to easily find i^m for fractional values of m using trigonometric functions:

\( i^m = cos(\pi / 2 \cdot m) + i \cdot sin(\pi / 2 \cdot m)\)

This is a pretty important and useful result.

We could stop here, but more whimsically, we can also move the scaling factor for m from right to the left, ending up with the following form:

\(i^{2/ \pi \cdot m} = cos(m) + i \cdot sin(m)\)

This is within an earshot of the well-known Euler’s formula:

\(e^{im} = cos(m) + i \cdot sin(m)\)

In that last equation, if we substitute m = π, the cosine expression becomes -1 and the sine expression becomes 0 (that is, e^iπ = -1 + 0i). Move the -1 to the other side and you end up with e^iπ + 1 = 0, which is deemed profound by many pop-science mystics and cranks. This is because it packs not one, not two, but five “special” constants in a single equality.

In all fairness to mystics, getting to Euler’s formula is not that simple: I skipped a step, and to explain the sudden appearance of the mathematical constant e, we’d need to do a bit more work. A rough outline can be found in the pinned comment under this post.

Postscript: the algebraic view

In most texts, complex numbers are introduced in a seemingly less purposeful way: not as a model of 2D geometry, but as a way to solve equations such as x² = -2. This seems somewhat fanciful: why is it important to have imagined “solutions” to such equations in the first place?

A good way to answer it is to start with the realm of natural numbers. Natural numbers are an intuitive formalization of rudimentary day-to-day math: one apple plus one apple equals two apples. That said, basic algebra on these numbers can produce solutions that lie outside the realm: for example, the solution to x + 2 = 1 is not a natural number. Because of this, we can say that natural numbers are not algebraically closed.

To fix the issue with subtraction, we can obviously extend the scheme by adding negative integers. We’re all used to the concept, but imagine defining it for a caveman mathematician! You’d probably say that we envisioned a make-believe realm of numbers that are just like naturals, except they’re coupled to a magic symbol to represent some multiple of the “negative unit” (-1). Oh and we came up with new rules for combining negative and positive values. Wait, doesn’t that sounds awfully close to the way we explain i?…

But I digress. The introduction of negative numbers solves subtraction, but still allows the realm to be escaped via division (the solution to 2·x = 1 is not an integer). To close that particular gap, we need to allow rational numbers. Yet, rationals are also not enough: the solution to x² = 2 is not a finite fraction.

Strictly speaking, we can fix this glitch in a more narrow way, but the usual “common-sense” upgrade from rationals are reals — which, in addition to irrational roots, also accommodate transcendental numbers such as (√2)^√2, π, or e. Reals are a familiar household name and seem to be on the brink of being algebraically closed… but then, what about x² = -2?

Well, we can address the issue by allowing the imaginary unit (√-1) — and crucially, this is where it all ends. The addition of this element closes off all escape routes from reals and gives us an algebraically-closed field. The only remaining gaps are singularities such as 0/0 (aka, 0·x = 0), which can’t have a well-defined solution under conventional algebra rules.

Just as importantly, the addition of imaginary numbers doesn’t break algebra: all the standard rules extend seamlessly to this realm. The only property we lose is strict ordering. To illustrate, assume that a = 1 + 0i and b = 0 + 1i. It’s clear that a ≠ b — but can we confidently say that a < b or a > b?

Either way: complex numbers are not just a one-off hack, but the final stepping stone in the construction of an escape-proof algebra system that naturally follows from observations about the real world. And yes: this means that standard algebra, taken to its logical conclusion, is a two-dimensional geometry.

👉 For a followup article about extending complex numbers to 3D, see here.

---

I write well-researched, original articles about geek culture, electronic circuit design, and more. If you like the content, please subscribe. It’s increasingly difficult to stay in touch with readers via social media; my typical post on X is shown to less than 5% of my followers and gets a ~0.2% clickthrough rate.