Not so fast, Mr. Fourier!

A real explanation of discrete Fourier transform (DFT, FFT), discrete cosine transform (DCT), and their inverses.

The discrete Fourier transform (DFT) is one of the most important algorithms in modern computing: it plays a key role in communications, image and audio processing, machine learning, data compression, and much more. Curiously, it’s also among the worst-explained topics in computer science. For example, the Wikipedia article on the matter assaults the reader with around three dozen cryptic formulas, but offers no accessible explanation how or why the algorithm works. More generally, most introductory texts focus on the purpose of the algorithm, not on what makes it tick.

My goal today is to change this. Let’s start with the basics: DFT takes a time-domain waveform — for example, an audio track — and turns it into frequency-domain data: a series of sine wave intensities that describe the underlying signal. If summed back together, these sine waves of different frequencies, phases, and magnitudes should faithfully recreate the original waveform.

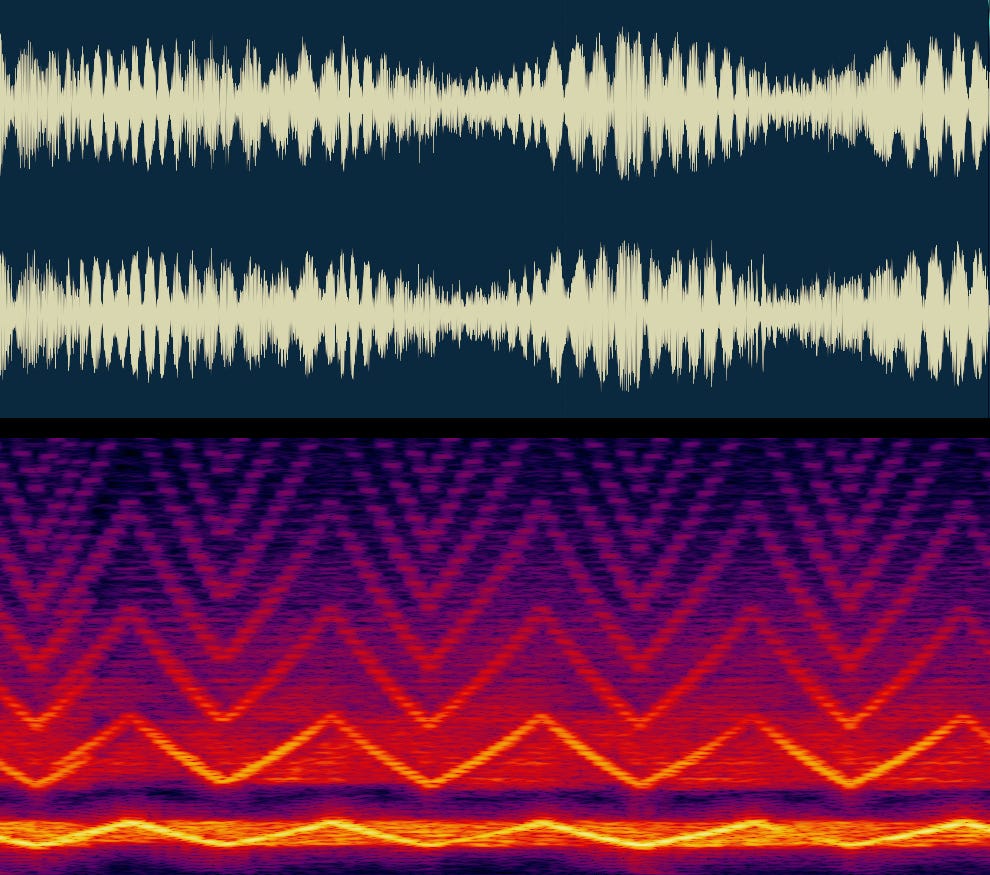
To illustrate the utility of DFT, let’s have a look at a conventional waveform representation of a 🔈 police siren next to its frequency-domain treatment. On both plots, the horizontal axis represents time. In the bottom image, the vertical axis represents frequency and pixel color represents intensity. The top view tells us very little about the recording; in the bottom plot, the shifting pitch of the siren is easy to see, at its base frequency and a number of harmonics:

Police siren: time-domain versus frequency-domain

Strictly speaking, the bottom plot — known as a spectrogram — is not the result of a single DFT operation; the transform doesn't show us how frequencies change over time. Instead, the spectrogram is created by dividing the audio into a number of short time slices and calculating a separate frequency-domain representation for each, each making up a column in the plot. This is sometimes referred to as a short-time Fourier transform (STFT); that said, this divergent terminology is of no real consequence, as the underlying math is the same.

Either way, the frequency-domain representation of signals allows us to perform a variety of interesting tricks. For example, when it comes to music, we can easily isolate specific instruments, remove unwanted AC hum, or pitch-shift the vocals. With the edits done, we can then convert the data back to to the time-domain waveform. Indeed, the infamous Auto-Tune pitch corrector, employed by some performers to cover up the lack of skill, is one of many applications of DFT.

But how does DFT work?!

To get it out of the way, let’s start with the official formula — which to a layperson, is rather opaque:

\(F_k = \sum\limits_{n=0}^{N-1} s_n \cdot e^{-i 2 \pi k\frac{n}{N} }\)

In this equation, F_k is the DFT value (“coefficient”) for a particular frequency bin k. Bin numbers are integers corresponding to a progression of frequencies. Moving on, s₀ to s_N-1 are the time-domain samples that make up the DFT input window; and the rest is… some voodoo?

To make sense of the voodoo, let’s conduct a simple thought experiment. Imagine a mechanical arm rotating at a constant angular speed. The arm is holding a pen that makes contact with a piece of drawing paper. The pen moves up and down the length of the arm in response to an input waveform.

Let’s assume that the arm is completing one rotation per second, and that the input signal is a sine wave running three times as fast (3 Hz). In this setting, the pen will end up drawing a neatly centered, three-lobed shape with every single turn:

A polar plot of a 3 Hz signal at an angular speed of 1 turn per second.

If you prefer, you can watch an animated version below:

Whenever the input frequency is an integer multiple of the arm turn rate, we always get a symmetrical, flower-like pattern in a single turn. The number of petals is equal to the ratio of frequencies.

If the input frequency is not an integer multiple — for example if the signal has a frequency lower than the turn rate — it will take multiple revolutions to produce a closed shape, and the lobes will end up intersecting. Still, the end result is similar; for example, here’s a pretty nine-lobed figure drawn in ten turns for a signal at 0.9 Hz:

A polar plot of 0.9 Hz at 1 turn per second (multiple turns).

Once again, you can watch an animation below:

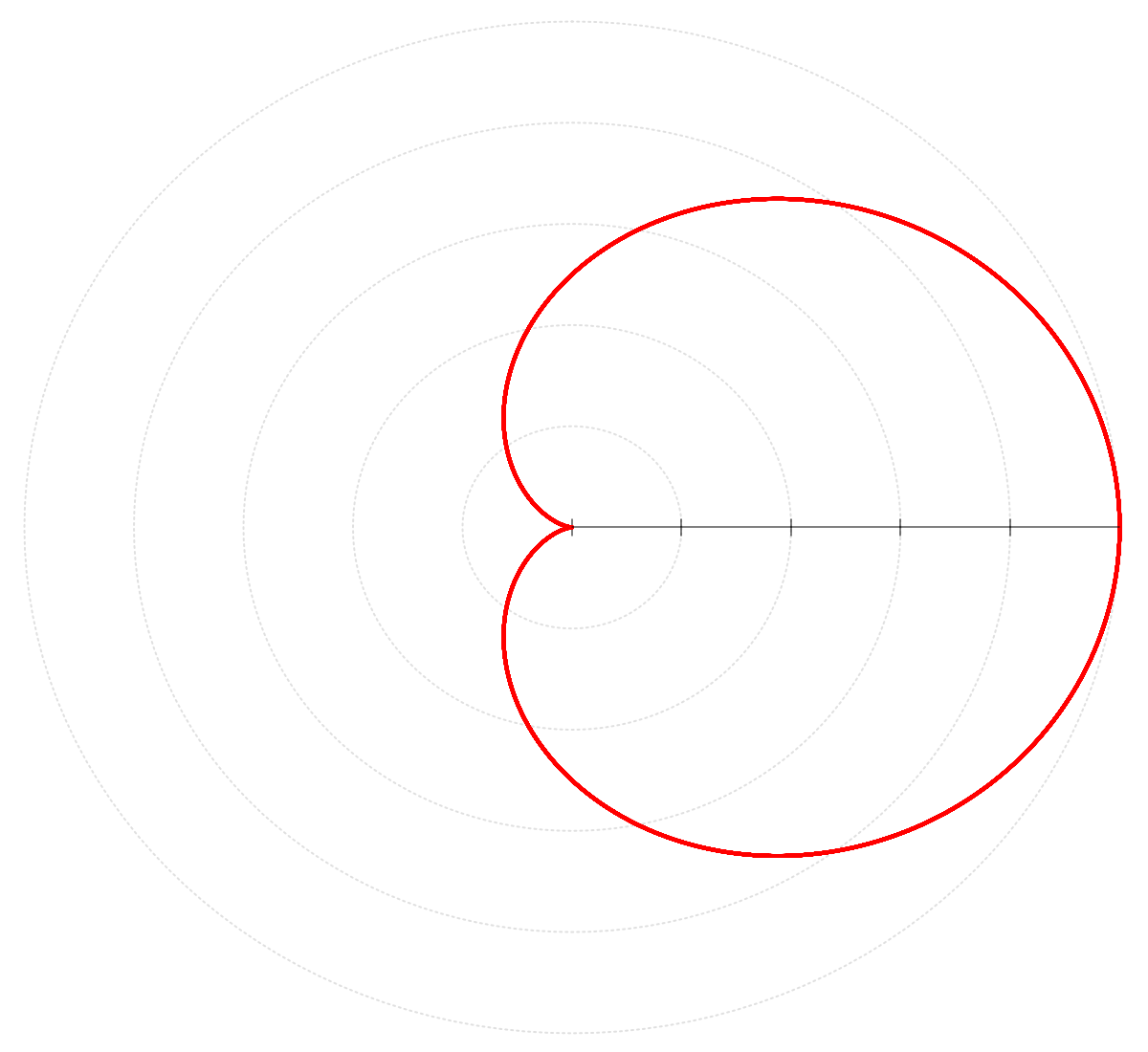
This radial symmetry crops up for every rational frequency ratio except for one special case: when the speed of the rotating arm matches the period of the sine waveform. In this scenario, the peak value of the input waveform always ends up on one side of the plot, while the valley stays on the other side:

1 Hz signal @ 1 turn / sec.

This single-lobed shape may end up being rotated depending on the phase of the input waveform, but one side is always sticking out.

Wondrously, this also works for composite signals consisting of superimposed sine waves. For example, if we take a 1 + 5 Hz signal, it will be off-center when plotted by an arm rotating at 1 Hz or 5 Hz — but will appear centered at 2 Hz:

Deconstructing composite signals. Blue dot is the center of mass.

In other words, we have a fairly ingenious frequency detector: we set the speed of the rotating arm, plot the samples — and if the results are not distributed evenly around (0,0), we know that there is a matching sine frequency component present in the input signal. We can even quantify the component’s magnitude by measuring the deviation of the shape from the center of rotation.

The discrete Fourier transform boils down to this exact operation. It takes a sequence of N values in the input window and distributes them radially in two dimensions at a given speed, completing k rotations. In the F₁ bin (k = 1), a single turn is used to distribute the entire span of the time-domain sample buffer — so if the buffer contains one second’s worth of data, the F₁ detection frequency would be 1 Hz. In the next bin (F₂), the rotational speed is twice as high, so in this particular example, the detector is tuned to 2 Hz — and so on.

For every bin, the formula sums the resulting coordinates of the distributed samples (that’s the ∑ part). The distance from the center of rotation to the computed midpoint is the magnitude of the calculated frequency component; the angle of the vector is the phase of the waveform. Note that some online sources, including a wildly-popular YouTube video, mistakenly state that the x axis component is the magnitude; this is incorrect.

This sample-distribution algorithm can be implemented with polar coordinates — angle and distance — mimicking what we did above. It can be done with Cartesian x,y coordinate pairs and simple trigonometry. The definition quoted at the beginning of this section does it in the most obtuse way possible — with a wacky device known as Euler’s formula — but all the methods are equivalent. The e^-i2πkn/N part is simply an apparatus for spinning things around in the complex plane by exploiting this surprising equality:

\(e^{it} = cos \ t + i \cdot sin \ t\)

If you’re unfamiliar with complex numbers, I have a primer here; in essence, it’s a way to encode x and y coordinates in a single variable by separating them with a magic-bean value of i = √-1. That said, we can avoid this complication altogether if we rewrite the DFT formula to use a pair of separate Cartesian coordinates — (x, y) — and then stick to standard trigonometry to implement rotations:

\(F_k =\Biggl ( { \sum\limits_{n=0}^{N-1} s_n \cdot cos ( 2 \pi k \frac{n}{N} )}, \ - { \sum\limits_{n=0}^{N-1} s_n \cdot sin( 2 \pi k \frac{n}{N} )} \Biggl )\)

This notation looks busy, but don’t panic. At a high level, it tells us that the value of each F_k bin is a pair of comma-delimited x-y coordinates: F_k = (x_k, y_k). Each coordinate is calculated using the sum operator (∑), which is just a fancy way of writing a run-of-the-mill for loop in mathematics: the operator runs from n = 0 to N-1 and adds the subsequent values of input samples (s_n), each sample multiplied by some additional trigonometric expression (more about that soon). We could expand the sums as:

\(\begin{align} x_k &= s_0 \cdot \textrm{<sth>} + s_1 \cdot \textrm{<sth>} + \ ... \ + s_{n-1} \cdot \textrm{<sth>} \\ y_k &= s_0 \cdot \textrm{<sth>} + s_1 \cdot \textrm{<sth>} + \ ... \ + s_{n-1} \cdot \textrm{<sth>} \end{align} \)

As for the <sth> part: before summing, each of the samples is multiplied by the sine or cosine of a particular timing expression. Within a single sum, the expression is constant apart from the n variable, which “ticks” as we move from one sample to another.

This core trigonometric operation — x = cos(t) and y = sin(t) — is a recipe to trace a circle with a radius of 1 as the parameter (t) goes from 0 to 2π (0° to 360° expressed in radians). In the specific timing expression used in the DFT formula, the 2π term is multiplied by k, in effect making sure that for bin k = 1, the apparatus distributes the samples across one full rotation; that it completes two rotations for k = 2; and so on. Finally, the n/N fraction just determines the successive radial position of each sample within these k turns.

A rudimentary implementation of DFT is straightforward; for example, in C, all you need is the following code:

void dft(complex* out_buf, complex* in_buf, uint32_t len) {

  for (uint32_t bin_no = 0; bin_no < len; bin_no++) {
    complex sum = 0;
    for (uint32_t s_no = 0; s_no < len; s_no++)
      sum += in_buf[s_no] * cexp(-2 * I * M_PI * bin_no * s_no / len);
    out_buf[bin_no] = sum;
  }

}

The code accepts and outputs complex numbers; for real number inputs, in_buf can be changed to double*. To convert the resulting complex coefficients in out_buf to magnitude, call cabs(). To get phase information (in radians), use carg().

Frequency limitations

Let’s start with the maximum frequency range. If the input data consists of real numbers, the DFT will produce useful output only up to the so-called Nyquist frequency — that is, one half of the sample rate. This frequency component can be found in the bin at k = N/2. The coefficients above that can and sometimes need to be computed — but perhaps a bit surprisingly, they just contain mirrored data from the lower-frequency bins.

To understand why this is happening, consider the following animation of our rotating arm. In the video, the arm is spinning so fast in relation to the input sample rate that successive samples are placed more than 180° apart. In fact, the angular distance is 330°, suggesting that we’re running the DFT at ~92% of the input sample rate:

After watching the clip, it should become clear that the end result is identical to what would be produced by a much slower arm spinning in the opposite direction.

The coefficient mirroring behavior is an artifact of the DFT algorithm, but the curse of the Nyquist frequency itself is not. It’s a fundamental bandwidth limitation for signal sampling techniques: above it, there’s simply not enough samples available to faithfully discern the frequency. The Nyquist limit is the reason why music is commonly recorded at ~44 kHz, even though our hearing only goes up to about 20 kHz (and only on a good day).

The other limitation of DFT has to do with frequency separation. A discrete Fourier transform that could use an infinitely-long sample window would have perfect selectivity — that is, it would be able to precisely discern chosen frequencies while rejecting everything else. In practice, DFT is run on finite sample windows, causing each bin to pick up something extra.

To understand the cause, let’s imagine we’re doing DFT with bins spaced three hertz apart — i.e., F₀ is the DC component, F₁ is 3 Hz, and F₂ is 6 Hz. The F₁ bin is always calculated by completing a single turn (the timing expression is k × 2π and k = 1). But if the input signal frequency is 2 Hz, we’d need three turns to form a closed, three-lobed shape that tells us “nope, this signal is not 3 Hz”. Instead, we run out of time after completing just a single, off-center lobe:

The limitations of DFT: a nearby frequency creeping into the F₁ bin.

In practice, the plot ends up badly off-center only if the two frequencies are quite close to each other. To illustrate, here’s an animation for our 3 Hz F₁ bin across a range of input signals. Watch the computed blue dot that tracks the “center of mass” of the shape — and thus represents the resulting DFT coefficient:

The dot is significantly off-center between 0.75 Hz and 5 Hz, but outside that range, it stays roughly where it’s supposed to be. As it turns out, the bias is significant only within roughly +/- 75% of bin step size. At lower frequencies, the partial shape is pretty close to a circle; at higher signal rates, it has enough symmetrical lobes that the missing part doesn’t upset the balance much.

We can measure this more rigorously. The following plot shows the average frequency response across all possible signal phases for a couple of 3 Hz-spaced bins:

Real-world DFT bin frequency response.

The overlaps mean that the standard set of DFT bins ends up accounting for the entire spectrum between DC and Nyquist. Nothing stops us from calculating ad-hoc DFT coefficients for any non-integer k in between, but these “partial-turn” bins don’t extract any new, finer-grained information from the system. If you need better frequency discrimination, you gotta up the sample rate.

Temporal limitations

This brings us to temporal resolution. A single DFT operation outputs frequency coefficients for the entire input waveform — and gives us nothing else. Within the time span it covers, we can no longer easily pinpoint when a particular tone start or ends, or whether its intensity is going up or down. Indeed, sharp signal discontinuities within the waveform produce wide-spectrum “halos” that are hard to interpret as any specific frequency. The more localized is the time-domain signal, the more ambiguous is its frequency-domain image.

This is why spectrograms divide the signal into short time slices and compute separate transforms for each slice, rather than performing one DFT for the entire buffer. But these slices can’t be arbitrarily short: at minimum, you must use a window large enough so that the bottom bin (F₁) aligns with the lowest frequency you wish to discern. To illustrate, if you have a 44.1 kHz audio stream and want to measure down to 20 Hz, you need a window of 44,100 / 20 = 2,205 samples — spanning 50 milliseconds — per each DFT.

A lot can happen within 50 milliseconds; it follows that various workarounds — such as the use of overlapping windows, weighted sampling, or specialized aliasing methods — might be necessary to get acceptable temporal resolution in certain applications. Audio processing tends to be one of them.

The inverse transform (IDFT)

The inverse discrete Fourier transform is conceptually simple. It boils down to generating waveforms for to every previously-calculated frequency bin, adjusting their magnitude and phase in accordance with the DFT-produced F_k coefficients, and then summing the results to recreate the contents of the time-domain sample window (s₀ to s_N-1).

Here’s the IDFT formula that does just that:

\(s_n = \frac{1}{N} { \sum\limits_{k=0}^{N-1} F_k \cdot e^{i{{2 \pi n \frac{k}{N} }}} } \)

Note the similarity of this equation to the forward DFT formula. There is an important symmetry in respect to inputs and outputs at the core of the algorithm; this is known as orthogonality. In a mildly mind-bending sense, the frequency domain is just the time domain turned “inside out”.

Here’s a simple implementation of IDFT in C:

void idft(complex* out_buf, complex* in_buf, uint32_t len) {

  for (uint32_t s_no = 0; s_no < len; s_no++) {
    complex sum = 0;
    for (uint32_t bin_no = 0; bin_no < len; bin_no++)
      sum += in_buf[bin_no] * cexp(2 * I * M_PI * s_no * bin_no / len);
    out_buf[s_no] = sum / len;
  }

}

As earlier, if working with real-number signals, out_buf can be declared as double* instead.

Remarkably, forward DFT followed by IDFT is lossless - i.e., it gets you the exact same time-domain data that you started with. In practice, some attention should be paid to the precision of floating-point calculations to avoid cumulative errors, but it’s usually not a big deal.

Understanding fast Fourier transform (FFT)

The DFT is perfectly adequate except for one tiny problem: even if we precompute the exponentiation part, the algorithm still involves K × N complex-number multiplications. Because the number of computed bins (K) is frequently the same as window size (N), some computer science buffs with a penchant for vagueness describe the computational complexity of DFT as O(n²).

This is where fast Fourier transform (FFT) comes to play; FFT is still a discrete Fourier transform and it produces the same results, but the calculation is cleverly optimized for large input windows and for the K = N use case (i.e., the algorithm can’t be used to selectively compute only some frequency bins).

The performance gains are due to a technique known as the radix-2 Cooley-Tukey algorithm. The derivation of this optimization is somewhat involved, but on a high level, it involves iteratively splitting the full DFT calculation into smaller sub-sums, and then exploiting the fact that the e^-i2πkn/N expression is periodic — it literally goes in circles! — to factor out many redundant multiplications. For larger windows, the resulting complexity of FFT approaches O(n ⋅ log₂ n), which is a pretty substantial improvement.

Numerous reference FFT implementations exist for almost every language imaginable; a particularly clean, minimalistic C implementation for power-of-two window sizes is as follows:

void __fft_int(complex* buf, complex* tmp, 
               const uint32_t len, const uint32_t step) {

  if (step >= len) return;
  __fft_int(tmp, buf, len, step * 2);
  __fft_int(tmp + step, buf + step, len, step * 2);

  for (uint32_t pos = 0; pos < len; pos += 2 * step) {
    complex t = cexp(-I * M_PI * pos / len) * tmp[pos + step];
    buf[pos / 2] = tmp[pos] + t;
    buf[(pos + len) / 2] = tmp[pos] - t;
  }

}

void in_place_fft(complex* buf, const uint32_t len) {
  complex tmp[len];
  memcpy(tmp, buf, sizeof(tmp));
  __fft_int(buf, tmp, len, 1);
}

Turning this code into inverse FFT (IFFT) boils down to removing the minus sign in the cexp(…) expression and dividing the final values by len.

Again, in practical applications, it would be wise to precompute the results of complex exponentiation; the value depends only on the pos index and the chosen window size.

DFT’s ugly brother: discrete cosine transform (DCT)

Discrete cosine transform can be thought of as a partial, real-numbers-only version of DFT. Just like discrete Fourier, it converts time-domain samples into a frequency spectrum. And just like DFT, it gets there by multiplying input data by cosine waveforms and then summing the results to obtain a bunch of binned coefficients.

That said, this description falls a bit short; the algorithm differs from discrete Fourier in a handful of interesting ways. First, let’s have a look at the usual formula for DCT-II, the most common variation of DCT:

\(F_k = \sum\limits_{n=0}^{N-1} s_n \cdot cos ( \pi k { n + \frac12 \over N} )\)

If you scroll back to the DFT equation, you might notice that in the formula above, k is multiplied by π (180°) instead of 2π (360°). In effect, the waveform-generating part uses an interleaved pattern of full-turn and partial-turn bins, running at half the frequency of DFT and putting F_N-1 at the Nyquist limit. This change isn’t just about being more efficient: if you try to switch the timing expression back to 2π, the entire algorithm goes sideways and many frequency bins start reading zero when they intuitively shouldn’t. In a moment, we’ll discuss why.

The other new element is the +½ offset in the timing expression. Recall that sample numbers run from n = 0 to N - 1, so dividing n by N leaves a gap on the upper end of the range. A +½ shift centers the waveform; the symmetry is important for making the inverse function work. Discrete Fourier doesn’t use this because its symmetry comes from the more basic relationship between cosine and sine in the complex plane.

The usual inverse DCT-II (IDCT-II) formula is:

\(s_n = \frac{1}{N} \sum\limits_{k=0}^{N-1} F_k \cdot w_k \cdot cos [ \pi (n + \frac12) {k \over N} ]\)

The w_k value is 1 for the DC bin (k = 0) and 2 for all the subsequent partial-turn bins (k > 0). You might encounter variants that put w_k and the scaling factor (1/N) in the forward DCT formula instead; heck, some authors split the factors between DCT and IDCT. These changes result in differently-scaled coefficients, but the overall operation is the same.

Now, let’s examine the fundamental mechanism of discrete cosine transform. Imagine we’re working with one second’s worth of data sampled at 2 kHz. With DFT, we get N / 2 = 1,000 usable frequency bins before hitting the Nyquist limit (1 kHz); bin spacing is 1 Hz. With the cosine transform, we’re getting N = 2,000 bins representing DC to Nyquist in 0.5 Hz increments.

Let’s pick the 4 Hz bin (F₈). First, consider what happens if we’re analyzing an input signal that’s running at 8 Hz. The image shows the reference 4 Hz waveform for the bin (blue), followed the input frequency (green), and then the computed product of the two (red). The product is centered around the x axis, so the DCT coefficient is zero:

DCT: mismatched frequencies.

But what if the frequencies (and phases) match? In the plot below, we’re still looking at the F₈ bin, but the input signal is now aligned at 4 Hz. The multiplication is always involving two positive or two negative values, so the product waveform now has a positive sum:

DCT behavior with matching frequencies and phases.

If the phases of the signals are off by half a cycle (180°), the discrete cosine transform still works — except the reading is negative.

Given the behavior observed here, one might wonder why we partook in all that complex-number chicanery that comes with real DFT. The answer becomes obvious if we consider the case of a 90° or 270° phase shift (one-fourth or three-fourths of a wavelength). In this situation, any detectable offset in the multiplied waveform simply disappears, and the F₈ coefficient is zero despite the presence of a matching signal frequency:

DCT bin #8 undone by a phase shift.

The original Fourier transform has no problem handling this case; at 90°, the DFT vector simply points up, the magnitude of the signal represented solely by the imaginary part (aka the y coordinate). In contrast, in discrete cosine transform, the imaginary part is AWOL, and we’re not registering anything in the expected frequency bin.

At this point, you might be wondering if the misaligned signals are simply lost. The answer is no — the genius of DCT is that the out-of-phase data ends up in the nearby “partial-turn” bins that are not computed in normal DFT. Sticking to our phase-shifted 4 Hz problem signal featured above, let’s peek into the next bin — F₉ at 4.5 Hz:

DCT partial-turn bin doing its job.

If you take a local view, the signal appears 90° out of phase at the beginning; seemingly snaps into phase in the middle; and then goes -90° out of phase at the end. Within this “partial-turn” bin’s measurement window, the average product is positive. If we go to the next “full-turn” bin (5 Hz), the product of the waveforms is once again zero because the composite waveform completes a full cycle.

In other words, DCT bins encode magnitude and phase information, just not always where we’re expecting it. This explains why the transform needs twice as many bins — and why trying to increase their spacing to match DFT breaks the algorithm.

This messy encoding scheme makes discrete cosine transform a fairly poor tool for most signal analysis tasks. That said, it’s great for fast, space-efficient compression algorithms where the aesthetics of the frequency-domain representation don’t matter much. A classic example is the JPEG image format, which performs DCT on 8×8 pixel tiles and then quantizes (i.e., reduces the precision of) the calculated coefficients to make them easier to compress using conventional lossless compression (Huffman coding).

Oh — if you wish to experiment with DCT-II, a simple implementation is included below:

void dct(double* out_buf, double* in_buf, uint32_t len) {

  for (uint32_t bin_no = 0; bin_no < len; bin_no++) {
    double sum = 0;
    for (uint32_t s_no = 0; s_no < len; s_no++)
      sum += in_buf[s_no] * cos(M_PI * bin_no * (s_no + 0.5) / len);
    out_buf[bin_no] = sum;
  }

}

void idct(double* out_buf, double* in_buf, uint32_t len) {

  for (uint32_t s_no = 0; s_no < len; s_no++) {
    double sum = 0;
    for (uint32_t bin_no = 0; bin_no < len; bin_no++)
      sum += in_buf[bin_no] * cos(M_PI * (s_no + 0.5) * bin_no / len) *
             (bin_no ? 2 : 1);
    out_buf[s_no] = sum / len;
  }

}

For a nonsensical but amusing demo that lets you watch what happens if you apply JPEG-style lossy compression to text, check out this post.

👉 If you’re interested in how DFT and DCT relate to the operation of radio receivers, check out this feature. For an article on alternative frequency domains, see here. For a thematic catalog of articles about electronics and signal processing, click here.

---

I write well-researched, original articles about geek culture, electronic circuit design, algorithms, and more. This day and age, it’s increasingly difficult to reach willing readers via social media and search. If you like the content, please subscribe!