Cursed circuits #2: switched capacitor lowpass

Still using resistors? Get on with the times.

In the previous post on this Substack, we looked at charge pump circuits and the mildly cursed example of a capacitor-based voltage halver. I find these topologies interesting because they are very simple, yet they subvert the usual way of thinking about what a capacitors can or cannot do.

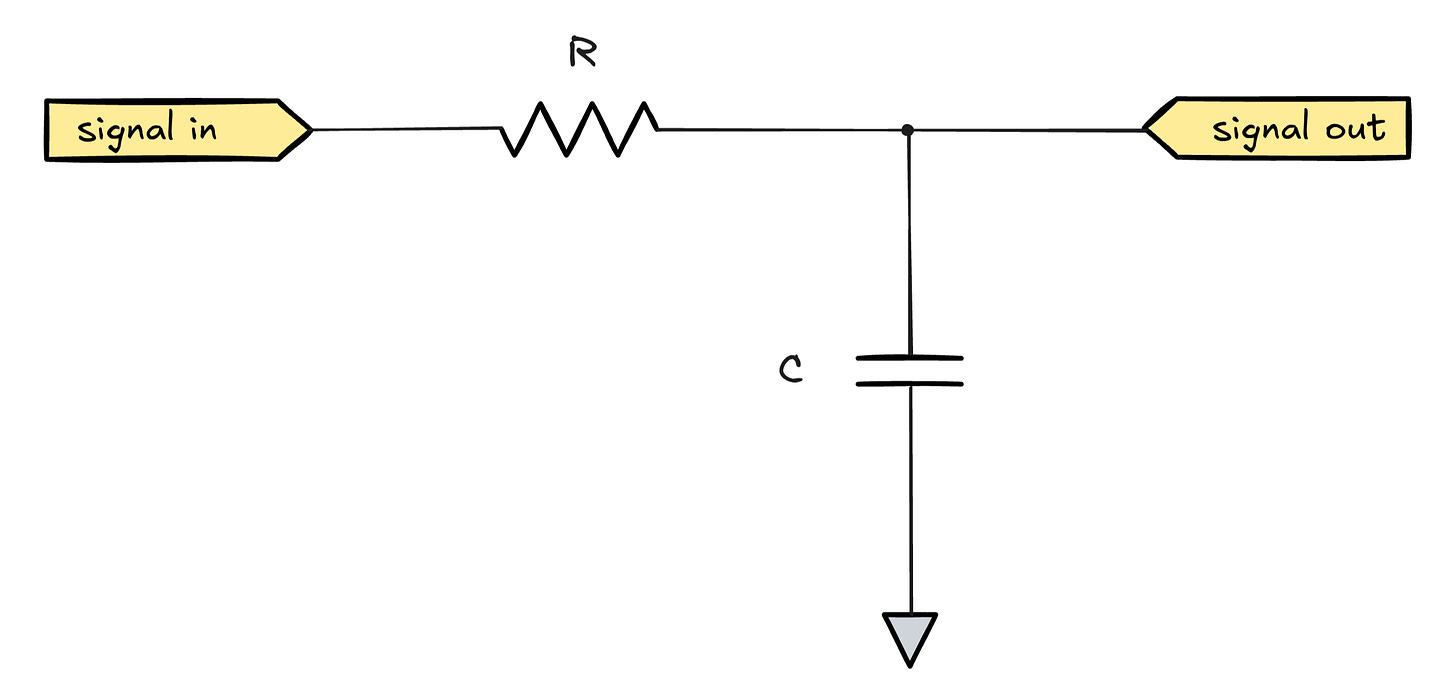
In today’s episode, let’s continue down that path and consider an even more perplexing example: a switched capacitor lowpass filter. The usual way to design an analog lowpass filter is to combine a resistor with a capacitor, as shown below:

A standard R-C lowpass filter.

The filter can be thought of as a voltage divider in which R is constant and C begins to conduct better as the sine-wave frequency of the input signal increases. This frequency-dependent resistor-like behavior of a capacitor is known as reactance and is described by the following formula:

\(X_C = {1 \over 2 \pi f C}\)

Most sources give this equation without explaining where it comes from, but it can be derived with basic trigonometry; if you’re unfamiliar with its origins, you might enjoy this foundational article posted here back in 2023.

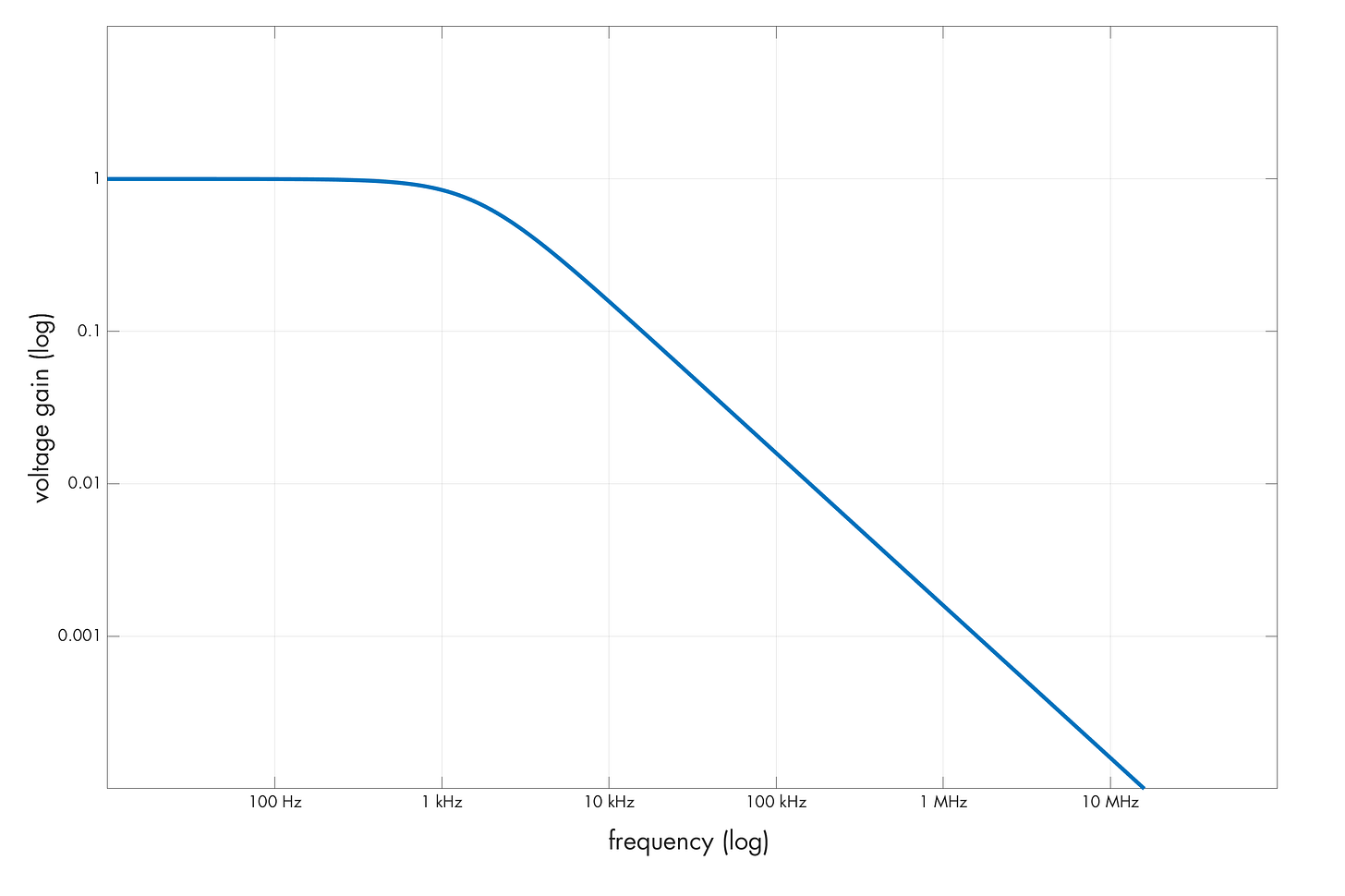
In an R-C lowpass circuit, the reactance is initially much larger than the value of R, so up to a certain frequency, the capacitor can be ignored and the input voltage is more or less equal to the output voltage. Past a certain point, however, the reactance of the capacitor becomes low enough so that the signal is markedly pulled toward the ground, attenuating it and producing a filter response plot similar to the following:

R-C lowpass filter behavior for R = 100 kΩ and C = 10 nF.

It’s easy to find the frequency at which R = X_C. The solution corresponds to the “knee” in the logarithmic plot shown before:

\(f_{knee} = {1 \over 2 \pi R C}\)

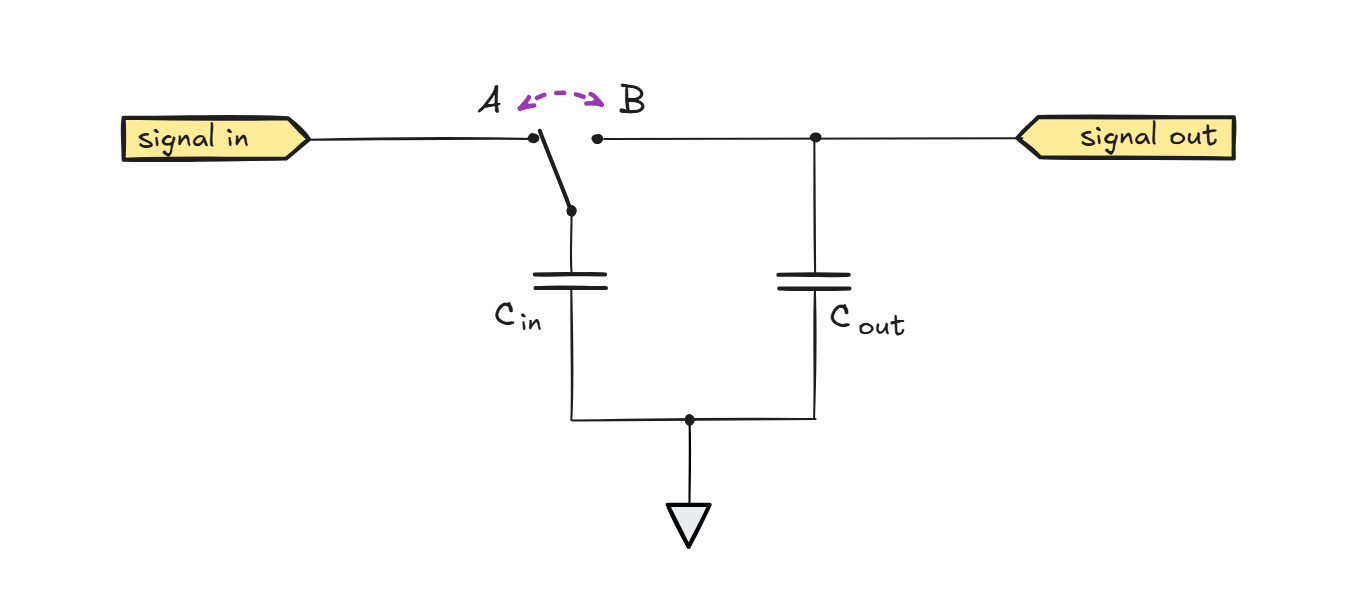
This is basic analog electronics, and something we covered on the blog before. But did you know that you can construct a perfectly good lowpass filter with a pair of capacitors and a toggle switch? The architecture is shown below:

A conceptual illustration of a switched capacitor lowpass filter.

In practical circuits, the “switch” would be a pair of MOSFETs driven by a timing signal, but nothing stops us from using a real switch or an electromechanical relay to experiment with this topology on a breadboard.

In the first half of the timing cycle, the switch is in position A. This connects a small input capacitor, C_in, to the input terminal. As soon as the connection is made, the capacitor charges to a voltage equal to the momentary level of the input waveform, which we can denote as V_A.

In the second half of the cycle, the two-way switch is moved to position B. This causes the voltages across C_in and C_out to equalize. We don’t need to solve for the relative shifts in their terminal voltages; it suffices to say that C_in started at V_A and ended up at V_B.

With this in mind, we can apply a a form of the fundamental capacitor equation (I = C·Δv/t) to find the average current that must have flowed out of C_in to shift its voltage by that amount in time t:

\(I_B = {(V_A - V_B) \ \cdot \ C_{in} \over t}\)

The switching period t is the reciprocal of the switching frequency f_s, so we can also restate this as I_B = (V_A - V_B) · C_in · f_s.

The formulas tell us that the average current is proportional to to the voltage present across the A and B terminals of the switch. The actual current is pulsed, but it otherwise looks like the ohmic behavior of a series resistor. In fact, from Ohm’s law, we can find the equivalent resistance that appears to be feeding C_out:

\(R_{in} = {V_{switch} \over I_{switch}} = {V_A - V_B \over I_B} = {1 \over C_{in} \cdot f_s}\)

If the circuit can be modeled as a series resistor feeding a shunt capacitor, we’re essentially looking at a bog-standard lowpass R-C architecture. The knee frequency of this R-C filter can be written as:

\(f_{knee} = {1 \over {2 \pi \cdot R_{in} \cdot C_{out}}} = {C_{in} \over { C_{out} }} \, \cdot \, {f_s \over { 2 \pi }}\)

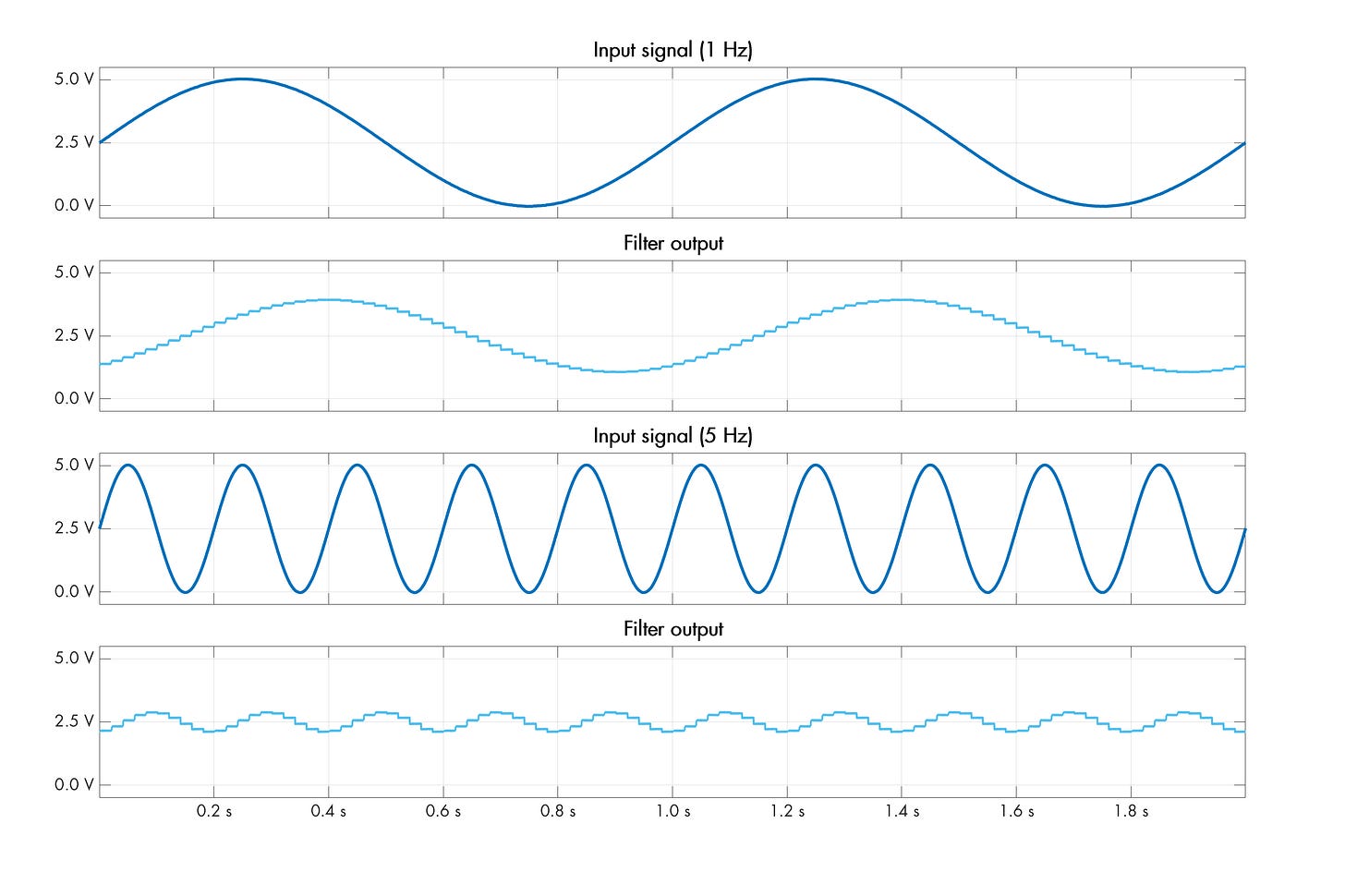
The math might seem improbable, but the circuit works in practice. The following oscilloscope traces show a filter constructed with C_in = 100 nF and C_out = 1 µF, toggled at f_s = 50 Hz. This corresponds to f_knee ≈ 0.8 Hz — and indeed, we see some attenuation for a 1 Hz input sine, and a lot more for a 5 Hz one:

A switched capacitor lowpass filter, showing variable attenuation.

The plot also offers an intuitive interpretation of the math: in each clock cycle, only a certain amount of charge can move between the capacitors; this corresponds to the maximum height of a single step in the output waveform, proportional to the relative sizing of the caps (i.e., the ratio of C_in to C_out). The larger the vertical step, the easier it is for the output waveform to track a fast-moving input signal.

The switching frequency f_s controls how many charge transfers occur per second, which gives us another method of controlling the filter’s center frequency: to shift it, we can speed up or slow down the supplied clock. That’s a major boon for digitally-controlled analog signal processing.

In practice, to minimize the stairstep pattern, we tend choose the switching frequency f_s to be about two orders of magnitude higher than the filter’s intended center frequency. To achieve this, from the earlier f_knee formula, we need to aim for C_out ≈ 16 · C_in.