The 101 of analog signal filtering
Some intuition about this topic can be developed without summoning the ghost of Pierre-Simon Laplace.
Signal filters are ubiquitous in electronics; on this blog alone, they cropped up in articles on digital-to-analog converters, radio receivers, audio amplifiers, and probably more.
In principle, the relative simplicity of these circuits should make the underlying theory easy to self-study; in practice, most introductory texts rapidly devolve into a foul mix of EE jargon and calculus. On Wikipedia, unsuspecting visitors are usually greeted by some variant of this:
“We wish to determine the transfer function H(s) where s = σ + jω (from Laplace transform). Because |H(s)|² = H(s)H(s)¯ and, as a general property of Laplace transforms at s = jω, H(−jω) = H(jω)¯, if we select H(s) such that:
\(H(s)H(-s) = \frac {{G_0}^2}{1+\left (\frac{-s^2}{\omega_c^2}\right)^n}\)The n poles of this expression occur on a circle of radius ωc at equally-spaced points, and symmetric around the negative real axis. For stability, the transfer function, H(s), is therefore chosen such that it contains only the poles in the negative real half-plane of s. The k-th pole is specified by …”
There are some aspects of signal processing that require solving novel integrals or navigating the complex S-plane — but in today’s article, let’s try a gentler approach. The following write-up still assumes familiarity with electronic concepts such as capacitance and reactance, so if you need a refresher, start here and here.
Prelude: charging and discharging a capacitor
Have a look at the following circuit:
Let’s assume that the capacitor is discharged and that the circuit’s input terminal gets hooked up to a standard, benchtop voltage supply. Further, let’s say there’s no load connected to the output leg.
If you’re comfortable with basic electronics, you can probably tell that the current through the resistor (blue) will initially shoot up to I = V/R because when the capacitor is discharged, the resistor is the only thing that stands in the way. Then, as the charge level increases toward the supply voltage, the current will gradually decay to zero:
Intuitively, the behavior sort of makes sense: a discharged capacitor is eager to sink any current you can spare, and there’s no way to move any more electrons onto the plates of a fully-charged one. But in between these extremes, what explains the exact shape of the voltage and current curves?
Well, it’s not that the capacitor is some sort of a nonlinear device! The blame is more on the resistor’s side: from Ohm’s law, the current flowing through it is always proportional to the voltage across its terminals. One leg of the resistor is connected to a fixed-voltage supply, so the potential on that side does not change; but the other leg “sees” the capacitor’s charge state, voltage rising over time. This reduces the current that will be admitted through that component (I = V/R). In effect, this negative feedback loop causes the resistor to progressively choke off the charging current, producing a pattern that looks like exponential decay.
There is a simple way to confirm this theory. If we connect the circuit to a benchtop supply operating in the non-default constant-current (CC) mode, the voltage across the capacitor will ramp up in a straight line — at least until the supply or the capacitor gives up:
In the constant-current scenario, the voltage across the capacitor’s terminal is simply equal to the charging current multiplied by the elapsed time, and then divided by capacitance:
This relationship follows from the fundamental definition of capacitance, as outlined this earlier article.
The solution for the R-C case is more complicated and would require some mathematical rigor to derive properly — but a bit of intuition and ingenuity will get us far. Let’s try to figure it out.
If you’re not interested in an accessible exploration of the R-C voltage formula, you can skip ahead to the paragraph marked with a “fast forward” pictogram (⏩).
We can start by constructing a simple discrete-time model where the capacitor voltage is “updated” at fixed intervals, and the current in each time slice remains const. For example, here’s a ten-step plot for R = 10 kΩ, C = 10 µF, and a supply voltage of 10 V:
In the initial 50 millisecond interval, the capacitor voltage is zero, so the resistor is subjected to the full supply voltage and admits 1 mA; as per the constant-current formula above, this charges the capacitor to 1 mA * 50 ms / 10 µF = 5 V. In the next interval, the voltage across the resistor’s terminals is reduced to 5 V, so the current is 500 µA, and the capacitor charges half as quickly. These current-halvings continue to infinity.
Of course, this is not reality — but despite the laughably low time resolution, this discrete-time model is remarkably close to the observed real-world behavior (dotted line). The example also shows pretty unambiguously that the current curve follows the pattern of exponential decay, with halvings every 50 ms. But how do we model that in continuous time?
On a high level, exponential decay is just the reciprocal exponential growth curve (y = 2t). The basic building block for that would be an equation along the lines of:
The formula models a signal that starts at y = 1 when t = 0, halves to y = 0.5 at t = 1, halves again to y = 0.25 at t = 2, and so on — with a limit of zero at infinity. This conceptually matches the behavior we observed earlier on.
Because the function runs from 1 to 0, to get closer to reality, we’d need multiply the values by the starting current, I(0):
What would that starting current be? Well, just like in the discrete-time model, at t = 0, the capacitor is fully discharged and has no voltage across its terminals. It follows that the momentary current from which the decay begins can be calculated from Ohm’s law: I(0) = Vsupply / R. That said, this is just to satiate curiosity; we don’t need to plug that in right now.
Our measurements and simulations indicate that the voltage curve is a mirror copy of the current curve: it starts at 1 and then tapers off to 0 over time. We can construct it by taking the exponential decay curve and subtracting it from 1. The result is:
We have the vertical aspect of the formula figured out right, but the timing is not right. The decay is a function of time, and quite obviously, the time to charge a capacitor must change in proportion to R and C: larger capacitors charge more slowly, doubly so if they’re charging through a larger capacitor.
From the basic capacitor equation (V=I·t/C) combined with Ohm’s law (I=V/R), the relationship between charging time and R and C is linear — so it stands to reason that the formula ought to be tweaked like so:
This tweak is conceptually sound, but if we compare it to empirical observations, the results will be a bit off — a fudge factor of ~1.4427 would need to be incorporated into the exponent for the values to match experimental results. We could settle for that, of course, but it’s good to understand why it’s this number in particular.
The issue in our formula is not actually the term in the exponent; it’s that we have no physical basis for the base value (2) in the exponentiation. I pulled the number out of thin air to provide an intuitive demo where halvings occurred every time the timing variable increased by 1. We’ve never established that this is how things work in a real R-C circuit; in the initial experiments, the halvings corresponded to 50 ms, not 1 s. As a matter of fact, it’s easy to show why base 2 is the wrong choice.
To illustrate the issue, let’s consider a scenario where Vsupply = 1 V, R = 1 Ω and C = 1 F. There’s nothing special about these values except their simplicity: there’s less number-wrangling if we go with that. In this model, from Ohm’s law, the initial, instantaneous current for a discharged capacitor at t = 0 should be:
Next, let’s imagine a vanishingly small time increment, Δt. The idea should be familiar if you read the earlier intro to capacitance and inductance. If not, think of it as a refinement of the discrete-time model: if Δt approaches zero, the discrete-time simulation approaches continuous-time reality. We don’t actually need to choose any specific value for Δt — we just assert that it is microscopic.
If we apply the fundamental capacitor equation (again, V = I·t/C), we can calculate that the cap will go from V(0) = 0 to the following voltage at t = 0 + Δt:
“Volts per second” crops up here as a consequence of the basic definitions of units: an ampere is equal to one coulomb of charge per second; a farad is equal to one coulomb per volt.
At this stage, we know V(0) and V(Δt), so we can calculate the rate at which the voltage is changing in the immediate vicinity of t = 0. Similarly to how velocity is the distance traveled divided by travel time, the rate we’re after is the change in voltage (V(Δt) - V(0)) divided by the size of the time increment (Δt). Let’s call that r(0):
A rate of one volt per second tells us that if we chart the voltage over time on a well-proportioned plot (1 V per vertical division, 1 s per horizontal division), the slope of the voltage curve near t = 0 should be exactly 45°.
This brings us back to the earlier, half-baked equation we’ve been trying to develop. We came up with the following:
In this case, because we’ve chosen the supply voltage of 1 V, R = 1 Ω, and C = 1 F, the formula can be simplified to just V(t) = 1 - 2-t.
We can quickly check if the formula matches the 1-to-1 rate of change we derived based on the fundamental equations. The simplest way is to do a numerical approximation. Again, the desired rate of change at t = 0 is 1, corresponding to an angle of 45° in a proportional plot. We can pick some small but definite Δt — let’s say 10-10 — and then just compute the rate implied by our speculative formula:
Oops — that’s pretty spectacularly off. We can also confirm the misalignment visually; it’s clear that the 45° diagonal (dashed line) that’s predicted by the fundamental formulas is not tangent to the y = 1 - 2-t curve in the eyeballed model of exponential decay:
In other words, we have a reasonably solid confirmation that base 2 doesn’t model the behavior of the RC circuit because it clearly violates the 45° constraint. Other bases produce exponential decay with different angles at t = 0 — but how do we find the right one?
Well, again we’re looking for base x that gives us the expected rate of change at t = 0: we need the equation to work out to r(0) = 1. The solution must follow this outline:
Assuming that 0 < Δt < 1, we can solve that last expression for x in a pretty straightforward way:
It’s not necessarily clear what that last equation converges to when Δt becomes infinitesimal, but we can make another numerical approximation:
If the numbers look familiar, it’s because the base that by definition gives a 45° slope at t = 0 happens to be well-known and well-defined: it’s the mathematical constant e, which is an irrational number equal to about 2.7183.
In fact, although e is usually introduced in a different way, the unique slope of ex (or e-x) is one of the constant’s most important properties. This is what makes e the natural choice for modeling processes that exhibit exponential growth or exponential decay:
In other words, it’s the only base that will give us a 45° start under the scaling-factor-free conditions discussed earlier on. The final and working formula for capacitor voltage is:
⏩ If you’re trying to skip the explanation of the RC formula, resume here.
The formula can be memorized, but it’s often enough to remember that at t = 0.7 RC, the capacitor is ~50% charged; at t = 3 RC, the process is about 95% done; and at t = 5 RC, the charge state is 99+%. Because R·C is the linear scaling factor for t, it’s sometimes called the “time constant” of this circuit.
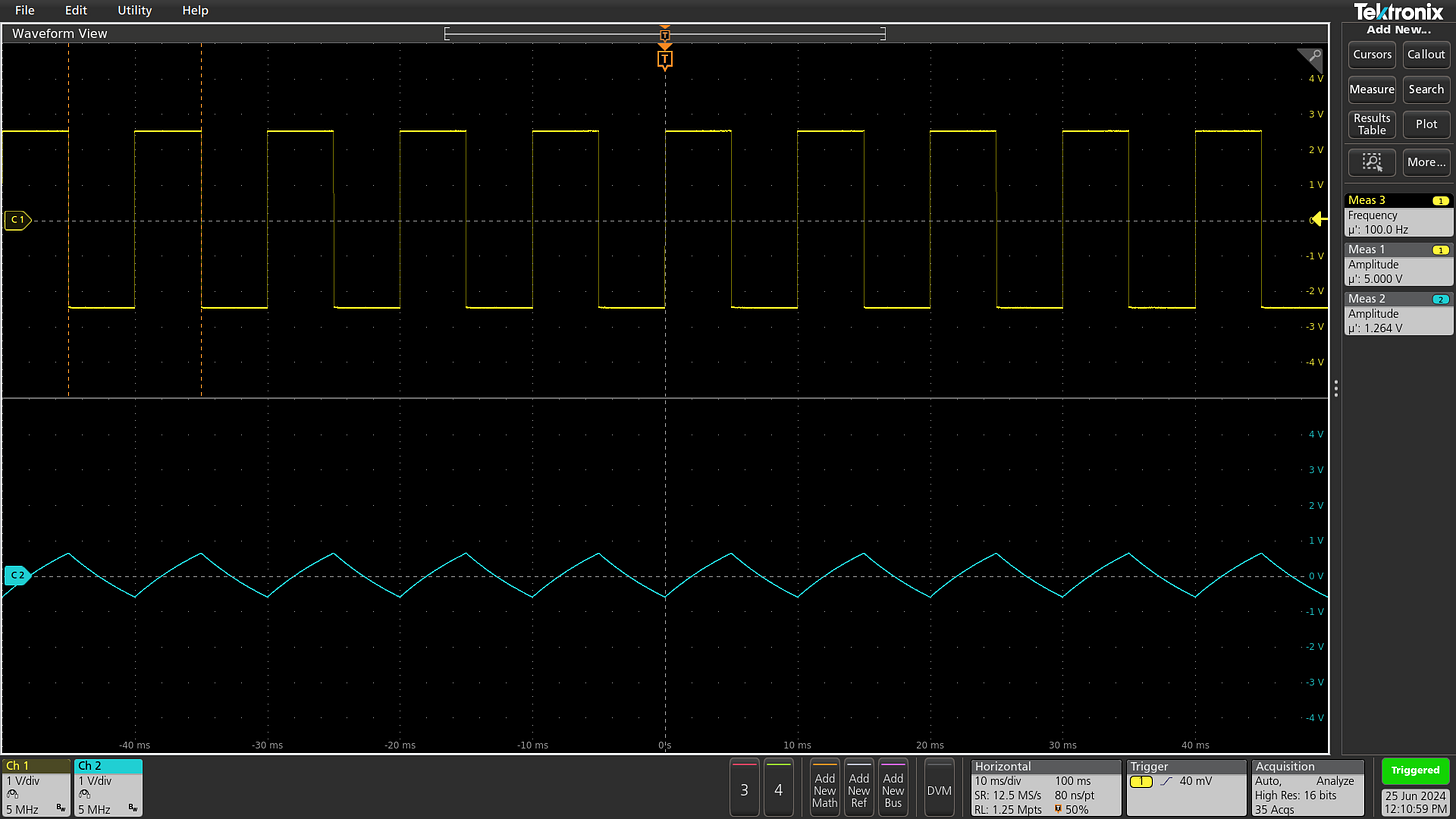
To validate our findings in practice, let’s assume R = 10 kΩ and C = 1 µF; as per the formula, 50% charge should be reached in ~7 ms. And indeed, we can easily observe this by supplying a 5 Hz square wave on the input leg:
At that frequency, the output still resembles the input, although the edges of the square wave are markedly rounded. At higher frequencies, the capacitor never charges to an appreciable extent, so the output amplitude is significantly attenuated — and the waveform consists only of the initial, nearly-constant-current portions of the charging slope:
The case of the sine waveform
The above R-C circuit is a lowpass filter: it lets low frequencies through while attenuating higher-frequency components. Some readers are probably expecting that I’m about to reveal the real lowpass filter: a better design that doesn’t distort the shape of the square waveform. But nope — for the most part, what we have here is the real deal.
As it turns out, most analog filters are relatively distortion-free only in one special case — a perfectly steady sine waveform:
This has a neat mathematical basis: the rate-of-change (differential) and the sum-over-time (integral) of a sine wave is a shifted sinusoid too; I have a simple geometric proof of this in an earlier article. This means that the only thing you can change with a combination of linear components is the amplitude, offset voltage, and phase of a steady sine wave. To turn it into a different waveform, you need some nonlinearity — a diode, a transistor, an inductor with a saturated core, and so on.
The mangling of non-sine waveforms by filters is not always an issue. In radio applications, the transmission is usually a sine signal; it is modulated, but the rate of modulation is much slower than the carrier frequency. In other words, in the local view, we’re dealing with a near-perfect sine, and the filter-caused distortion is negligible.
In audio and video, the signals are seldom pure sines; for example, many instruments produce sounds closer to sawtooth or square waves. That said, the distortion produced by analog filters tends to mimic natural phenomena. As a practical example, audio equalizers are useful for compensating for the acoustics of the listening environment even if they don’t do anything especially logical to the notes played on a trumpet or a viola.
In other cases, the distortion can’t be ignored, but it can be quantified and accounted for. Even if one is not proficient with calculus, it’s usually sufficient to recast more complex waveforms as a sum of sine harmonics. This is trivial for square waves — and fairly straightforward in the more general case, too.
But back to the lowpass filter…
Right! The sine wave scenario is neither constant voltage nor constant current, so the capacitor charge formulas discussed at the beginning of this article are not directly relevant. Thankfully, the solution for sine waves is actually simpler. Let’s start by imagining what would happen if we replaced the capacitor with another resistor, R2:
This is essentially a voltage divider. From basic circuit laws, the current flowing through the both resistors must be the same. Series resistances sum in a straightforward way, so from Ohm’s law, this end-to-end current is IR1,R2 = Vin/(R1+R2). Vin stands for the externally-supplied voltage on the input leg.
Now, let’s consider R2 specifically. Again, from Ohm’s law, the voltage that will develop across it is proportional to current and resistance: VR2 = IR1,R2·R2. Because the resistor is connected between the output pin and the ground, this means that Vout = IR1,R2·R2. Combining the equations, we get:
Now the fun part: recall from the discussion of impedance that a capacitor in the presence of a sine wave signal exhibits behavior that resembles frequency-specific resistance. It’s known as capacitive reactance and is described by the following formula:
Perhaps, for a given sine frequency f, we could treat the filter as a voltage divider formed by R and C?
Well, yes and no. Resistance and reactance are just abstractions around voltage and current, representing a deconstruction of a signal into in-phase (0°) and orthogonal phase-shifted (90°) components. If we have a sinusoidal current, to isolate resistance, we’d take voltage measurements at the time the current is peaking; meanwhile, to figure out reactance, we’d be measuring voltage one-fourth of a period earlier. Because they describe different points on a sinusoid, R and X don’t sum the obvious way.
Luckily, we analyzed this exact scenario in the earlier article on complex impedance, and tipped some triangles to to come up with a formula for the sum of R and X. It’s the square root of the sum of squares. In the end, all we need for the R-C voltage divider is a small tweak in the denominator:
The resulting output signal will have some intermediate phase shift in relation to the input voltage, ranging from nearly nothing at DC and approaching lag of one-fourth of a cycle (-90°) as very high frequencies.
We’ll circle back to phase shifts soon. For now, let’s plot this equation across a range of sine wave frequencies for R = 10 kΩ and C = 1 µF:
The curve may seem a bit weird, but that’s just a graphing quirk. The attenuation behavior doesn’t taper off at high frequencies; it just looks this way because on a linear scale, the visual distance between 100% and 50% is much larger than between 10% and 5%. To avoid confusion, it’s more common to use log-log scale:
We can see that this particular filter lets through frequencies up to about 8 Hz with little attenuation. Then, there’s a fairly pronounced knee down to around 25 Hz, followed by a fairly straight slope. On that slope, with every doubling of the signal frequency, the amplitude of the output signal is halved.
(Electrical engineers like to obscure this simple relationship with weird mixed units such as “-20 dB per decade” or “-6 dB per octave”. It’s the same thing.)
In the filter, R is constant; meanwhile, XC approaches infinity at 0 Hz and then decreases with signal frequency. The combined impedance to the ground is dominated by the resistive effects below a certain frequency, and then by the capacitive shunting to the ground above that:
At some specific sine frequency fc, the two values briefly become equal; this is the crossing point in the plot above. We can find this crossover point pretty easily:
Unsurprisingly, this is also the midpoint of the filter’s phase shift (-45°).
From the earlier formula for voltages, we can see that at this exact location, the input signal is attenuated to √½ (~70%, -3 dB) of the original amplitude:
Now, a word of caution: there’s a somewhat arbitrary convention to refer to the ~70% point of a filter as the cutoff frequency. For this particular circuit, the cutoff frequency coincides with the solution for R = XC. But in other types of filters, they might not overlap! Beware of ambiguity on the internet.
For what it’s worth, although the ~70% cutoff point (f-3db) has some nice mathematical properties, we can also solve the formulas for 50% attenuation, or any other point of our choice. For 50%, the calculation is:
And the associated 50% amplitude reduction frequency is:
You mentioned phase shift?
Yes. In the earlier articles, we talked about capacitors, inductors, and RC, RL, or LC circuits as causing current-to-voltage shifts. But in this instance, we’re saying there’s a phase shift between the input voltage (Vin) and the output voltage (Vout). Before we proceed, it might be useful to ask why.
The first half of the answer is that, as discussed earlier in the article, there is a common sinusoidal current flowing through the series R-C path to the ground. Our earlier analysis of the series R-C circuit showed that the current is shifted left by some variable, frequency-specific amount.
In the article linked in the preceding paragraph, have the derived the following formula that describes the offset that needs to be incorporated in the voltage expression to model this behavior:
Alternatively, if we take the voltage waveform to be the ground truth, we can also calculate the positive offset for current. It’s the same number with a flipped sign:
In most software, you’ll get the result in radians; multiply it by 180°/π for degrees.
In essence, the voltage is nearly one-fourth of a cycle behind the current (-90°) as we approach DC, and then falls more or less in line (0°) by the time the frequencies are well above the circuit’s fc.
But hold on — this sounds pretty much like the opposite of how I described the lowpass filter. I asserted that the output of a lowpass RC filter has a shift of close to 0° around DC, and that Vout eventually falls behind and approaches -90° at high frequencies. This has to do with what we’re measuring and where: in a filter, we’re not interested in the common R-C current to the ground. What we’re after is the phase shift between two voltages: Vout and Vin.
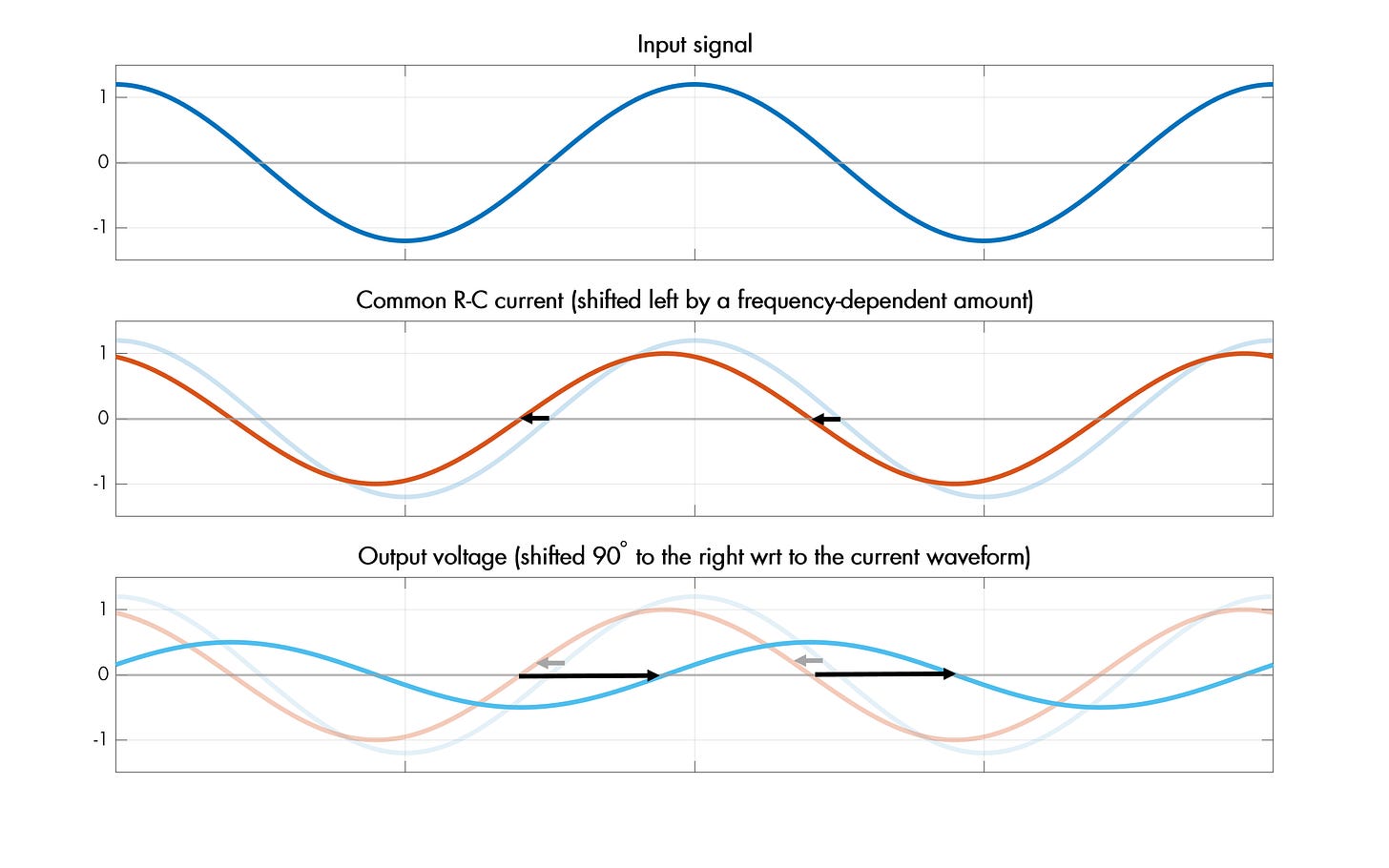
Again, there is a common current flows through both R and C; as noted above, the timing expression is shifted in relation to the input voltage by a positive amount, θI to V. But then, it is a fundamental property of capacitors that the applied current always produces a voltage across the terminals that lags the current by exactly one-fourth of a cycle (-90°). The capacitor sits between GND and the output pin, so this shifted voltage is what we’re looking at as the output of the filter:
To put this differently, we first created a current that was shifted by some frequency-specific amount n to the left of the input voltage; and we then tapped into a voltage that’s necessarily shifted one-fourth of a cycle to the right of said current. We moved by n in one direction and then by 90° in another. The result is the same as a single move by -90° + n.
We could just tack this onto the earlier RC phase shift formula, but a basic geometric analysis (or a quick peek at Wikipedia) tells us that arctan(x) - 90° is the same as -arctan(1/x), so a simpler version of the equation is:
Plotting this over a range of frequencies for our example lowpass filter nets us this:
The general formula for a frequency at which you can observe a certain voltage phase shift θ (again, typically radians) is:
It’s important to underscore that the RC circuit is not a real signal delay mechanism; the apparent Vout lag is just a consequence of the components transforming the sine wave in a particular way. With other waveforms, the output of an RC filter wouldn’t be phase-shifted. Instead, it would get mangled in funny ways.
Taking the high road
A highpass filter that attenuates low frequencies can be constructed similarly to the lowpass — all we have to do is switch the capacitor and the resistor around:
In this layout, the capacitor admits only rapidly-changing currents, but blocks DC. The sine wave behavior is essentially identical (but inverse) to that of the lowpass circuit; this includes the same formula for fc at R = XC.
The behavior with non-sine waves is another matter. A high-frequency square wave signal will pass through with edges intact, but some (exponential) DC voltage decay in between:
At low frequencies, the signal is more severely mutilated — only the edges remain, appearing as short voltage spikes of alternating polarity:
The most intuitive way to explain this pattern is to take a closer look at the dynamics of a capacitor. For energy to be stored in this component, there must be a symmetry in the motion of charges flowing onto and off the plates. This way, the resulting electrostatic fields – increasingly positive on one plate and increasingly negative on another – largely cancel out, allowing a non-trivial charge to be stored with ease.
If one of the capacitor’s is left floating, the device can’t be charged or discharged with ease; instead, its previous charge state persists. If we take a capacitor charged to 1 V and connect one of its legs to a 10 V supply, the free-floating leg will read 11 V in reference to the ground. If we connect it to a -5 V supply, we’ll get a reading of -4 V. The behavior is no different from putting a battery in series with another voltage source.
From the perspective of fast-changing signals, the highpass filter resembles a capacitor with a free-floating leg. This is because the resistor to the ground can’t supply charging currents quickly enough for it to matter; if the input voltage suddenly jumps, the charge state doesn’t change, and the circuit’s output terminal shifts in tandem with the step change in the input voltage.
At the same time, on longer timeframes, the resistor does allow the capacitor to gradually charge. If the input voltage is a steady 2.5 V and the resistor is tied to the ground, the capacitor will eventually reach Vcap = -2.5 V (as measured from left to right), causing the output voltage to decay to zero. As discussed earlier, this process takes about t ≈ 3·RC.
Some time later, when the input voltage jumps from +2.5 V to -2.5 V, the output moves in tandem with this, producing a -5 V spike followed by exponential decay. The pattern of five-volt spikes continues from that point on.
The knowledge of this pattern is useful for spotting accidental highpass filters in the circuit. This can happen when a series “capacitor” is formed by a broken wire or a cold solder joint on a digital data line.
Higher-order filters
The filters discussed so far exhibit fairly gentle frequency rolloff behavior. This is in contrast to an idealized “brick wall” filter, which should pass through everything on one side of a chosen frequency, and then completely block everything on the other side.
The angle of the frequency attenuation slope can be increased by stacking RC filters in series. That said, this inevitably increases attenuation in the filter’s “pass” region, increases phase shift — and still leaves a relatively pronounced, rounded knee around the cutoff frequency.
The common solution to this problem is to make the filter somewhat resonant in the vicinity of the cutoff frequency — be it with an extra inductor or an op-amp feedback loop. In the presence of a steady sine signal, the approach adds a region of apparent amplification due to the constructive interference between the current signal and the echo of the previous cycle. This makes the knee more “pointy”, although at the expense of the filter behaving even more chaotically if presented with something that isn’t a well-behaved sine.
The design of such filters is where the math gets heavy. Insufficient dampening or poor phase characteristics can yield wildly inconsistent frequency response curves — or even sustained oscillations. That said, most of the time, filter design is done by following “cookbook” formulas based on already-proven theorems and pre-solved calculus. Of special note is the Butterworth filter formula, offering the optimal filtering characteristics if you can’t tolerate frequency response ripples; and the Chebyshev filter, which offers the best performance for a chosen amount of ripple on one end.
👉 For a continuation dealing with more advanced op-amp filters, click here. For switched capacitor filters, check out this article. For a thematic catalog of posts on this site, click here.
I write well-researched, original articles about geek culture, electronic circuit design, and more. If you like the content, please subscribe. It’s increasingly difficult to stay in touch with readers via social media; my typical post on X is shown to less than 5% of my followers and gets a ~0.2% clickthrough rate.
















This is a really nice and gentle introduction.
It is worth introducing the fact that capacitors especially are non-ideal. In an intro, that can be an offhand remark, but as soon as somebody leaves the audio frequencies, this becomes a really big deal. A 10µF capacitor, for instance, can easily have a self-resonance well below 1MHz. Without understanding parasitics, all kinds of real-world circuit behavior is highly mysterious. With a simulator in hand and some decent models for imperfect components, this is much easier.
I made a video just now on some testing I did because of how hard this bit me:
https://www.youtube.com/watch?v=fsE0bIpDPeU
Man I wish someone explained low high and bandpass filters like this when I was studying EC engineering.
Really liked this post.
I would like to share some more interesting topics you can explore if you are interested.
1. Control systems, PID controllers and how they can implemented...
2. Difference between single mode optic fibre and multi mode optic fibres. How they are used in industry.
3. The process of semiconductor fabrication and how etching is performed.
If you are comfortable I am willing to write a post for you to share on satellite communication and topics like orbital dynamics and attitude, altitude adjustment of satellite systems.