How has mathematics gotten so abstract?

What's the meaning of "numbers" and "arithmetic operations"? We consult Georg Cantor's turtles and look at Giuseppe Peano's code.

Today, mathematics is regarded as a supremely abstract science. On forums such as Stack Exchange, trained mathematicians may sneer at newcomers who ask for intuitive explanations of mathematical constructs. Indeed, persistently trying to relate the foundations of math to reality has become the calling card of online cranks.

I find this ironic: for millennia, mathematics was essentially a natural science. We had no philosophical explanation why 2 + 2 should be equal to 4; we just looked at what was happening in the real world and tried to capture the rules. The abstractions were important, of course, but they needed to be rooted in objectivity. The early development of algebra and geometry followed suit. It was never enough for the axioms to be internally consistent; the angles of your hypothetical triangle needed to match the physical world.

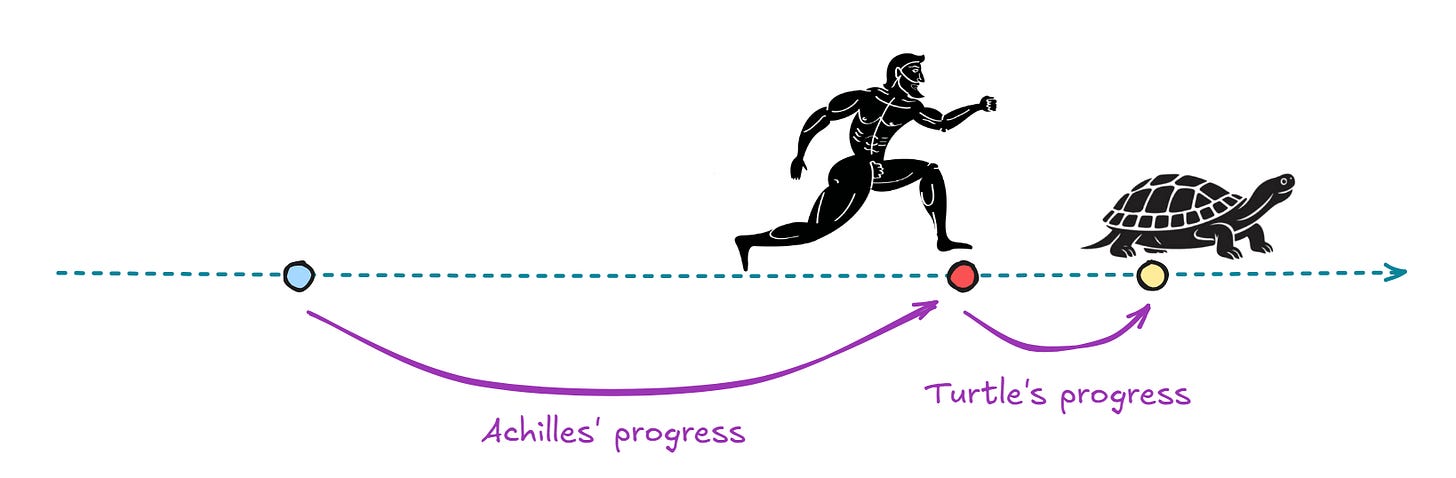
That said, even in antiquity, the reliance on intuition sometimes looked untenable. A particular cause for concern were the outcomes of thought experiments that involved repeating a task without end. The most famous example is Zeno’s paradox of motion. If you slept through that class, imagine the scenario of Achilles racing a tortoise:

Catch me if you can.

We can reason that after a while, Achilles will catch up to the turtle’s original position (red dot); however, by the time he gets there, the animal will have moved some distance forward (yellow dot):

And they would have gotten away with it too…

Next, consider the time needed for Achilles to reach the yellow dot; once again, by the time he gets there, the turtle will have moved forward a tiny bit. This process can be continued indefinitely; the gap keeps getting smaller but never goes to zero, so we must conclude that Achilles can’t possibly win the race.

Amusingly, the problems caused by infinity lingered on the periphery of mathematics for centuries, fully surfacing only after we attempted to fix them with calculus. Calculus gave us a rigorous solution to the ancient puzzle: an infinite sum of time slices can be a finite number, so Achilles does catch up to the tortoise. Yet, to arrive at that result, the new field relied on the purported existence of infinitely small numbers (infinitesimals). The founders struggled to explain how to construct such entities, where to find them on the real number line (you can’t), and whether they’re safe to mix with real number algebra in the first place.

Over time, this prompted a number of mathematicians to try and build a more general model of mathematics, starting from the ground up — that is, from the principles of formal logic. In particular, one prominent faction of the movement sought to define numbers and arithmetic operations in a way that was fully independent of the physical realm.

By golly, Mr. Peano, it all adds up

In the late 19th century, Giuseppe Peano successfully answered this call. His system posits the existence of a single initial number — conventionally, zero — and then defines a successor function S.

This allows us to define numbers — really, just a collection of labels — solely in terms of a succession relationship:

\(\begin{alignat}{1} 1 &= S(0) \\ 2 &= S(1) &&= S(S(0)) \\ 3 &= S(2) &&= S(S(S(0))) \\ 4 &= S(3) &&= S(S(S(S(0)))) \end{alignat}\)

While this might seem mundane, the scheme reduces many other problems to the process of induction and recursion. For example, to solve 2 + 2, we don’t need any a priori knowledge of what “2” or “+” means. Instead, we define addition using the following two rules:

\(\begin{alignat}{1} a &+ 0 &&= a &&\qquad (\textrm{rule 1}) \\ a &+ S(b) &&= S(a+b) &&\qquad ( \textrm{rule 2}) \end{alignat} \)

This notation may appear abstract, so to tease it out, let’s try to actually calculate 2 + 2. Because the second operand is non-zero, we can’t apply the first rule just yet. That said, from the construction of Peano numbers, we know that 2 = S(1). In light of this, we can rewrite 2 + 2 in a way that lets us use of the second rule:

\(\begin{array}{r l} 2 + 2 = 2 + S(1) & \textrm{(by the construction of number 2)} \\ 2 + S(1) = S(2 + 1) & \textrm{(per rule 2)} \end{array}\)

At this point, we’ve shown that 2 + 2 is the same as S(2 + 1). To solve the original equation, we still need to find the value of 2 + 1; this can be done by applying the same substitution technique once more:

\(\begin{array}{rl} 2 +1 = 2 + S(0) & \textrm{(by construction)} \\ 2 + S(0) = S(2+0) & \textrm{(per rule 2)} \end{array}\)

In effect, we have restated 2 + 2 as S(2 + 1), and then 2 + 1 as S(2 + 0). In that last instance, the second operand is zero, so we can finally apply rule 1. The rule says that a + 0 = a, so:

\(2 + 1 = S(2 + 0) = S(2)\)

Further, from the construction of Peano numbers, we know that our chosen label for S(2) is 3; therefore, 2 + 1 = 3.

With this equality established, we go back to the initial step where we expressed 2 + 2 as S(2 + 1) and get the final answer:

\(2 + 2 = S(2+1) = S(3) = 4\)

If you work with software, you might appreciate the following C code that implements roughly the same logic (demo):

#include <stdio.h>

struct number { char* label; struct number* next; }
  five  = { "5", NULL },   four = { "4", &five }, three = { "3", &four },
  two   = { "2", &three }, one  = { "1", &two },  zero  = { "0", &one };

struct number* succ(struct number* num) { return num->next; }

struct number* pred(struct number* num) {
  struct number* ret = &zero;
  while (succ(ret) != num) ret = succ(ret);
  return ret;
}

struct number* add_numbers(struct number* num_a, struct number* num_b) {
  if (num_b == &zero) return num_a;
  return succ(add_numbers(num_a, pred(num_b)));
}

int main() {
  printf(”2 + 3 = %s\n”, add_numbers(&two, &three)->label);
}

In this program, instead of relying on built-in integers, we start with a unidirectional linked list of strings: “0” → “1” → “2” → “3” → “4” → “5”. This data structure encodes the successor relationship between the labels without giving them any further meaning.

Next, we define a trivial helper called succ(x), which returns the successor of x, along with a slightly more complicated function called pred(x), which finds the element to which x is the successor. Finally, add_numbers(a, b) is a straightforward implementation of the recursive rules for Peano addition, as outlined earlier on.

Again, the merit of this approach is that it lets us model arithmetic without any external assumptions about the nature of numbers, the significance of the addition operator, and so forth. We used familiar labels (0, 1, 2, 3, 4, …), but we could’ve used some other ordered collection of abstract symbols (🥔, 🎵, 🐸, 🌀, 🐱, …). If so, we’d have gotten an equivalent model of math in which 🐸 + 🐸= 🐱.

Of course, Peano arithmetic is too cumbersome for everyday tasks; instead, it serves as a minimalist model for theoretical work. It is used similarly to how computer scientists use Turing machines; no one wants to browse the internet on a Turing-style computer, but if you proved that P = NP for a Turing machine, this would have implications for more practical computing architectures too.

Numbers from sets

Giuseppe Peano’s axiomatic approach was revolutionary and led to breakthroughs such as the Gödel incompleteness theorem; however, it still didn’t offer a particularly good model of infinite quantities. For that, mathematicians needed to turn to an even more exotic framework: set theory.

In set theory, numbers are conventionally defined as labels for specific, ordered sets. To get started with the construction process, we only need an empty set ({}), which we label as zero:

\(0 = \{\} \)

To define the successor number, we add an element to the set. To avoid inventing arbitrary new elements, we can simply embed the previously-conjured number zero in the successor set:

\(1 = \{0\}\)

If this seems confusing, you can think of sets as boxes. We started with an empty box with zero items inside; we then sealed the box and placed it in a larger container, so the larger box now contains a single element. For this tally, the contents of that smaller, sealed box are of no consequence.

After that, we can’t define the next successor as {0, 0}; this is because in set theory, every set element must be unique. That said, as discussed earlier, a “naked” element n is distinct from a box containing that element (i.e., a new set {n}), so we can do this:

\(2 = \{0, \{0\}\} \)

Note that in our model, 1 = {0}, so the construction method shown above is equivalent to saying that 2 = {0, 1}.

To get to the third successor, we need to put one more element in the set. At this point, we can’t reuse 0 or 1, but we can embed the recently-created set representing 2:

\(3 = \{ 0, 1, 2 \} = \{ 0, \{ 0 \}, \{ 0, \{ 0 \} \} \}\)

This process can continue for as long as we’d like, e.g.:

\(4 = \{ 0, 1, 2, 3 \} = \{ 0, \{0\}, \{0, \{0\}\}, \{0, \{0\}, \{0, \{0\}\}\} \} \)

In set theory, the labels we’re creating are called ordinals. Note that every ordinal is an ordered set of all the preceding ordinals, and that the set never contains itself.

If you’re seeing parallels to the iterative construction of Peano numbers, this is not an accident; the two approaches are conceptually similar, it’s just that in this instance, the underlying mathematical structure of each number is spelled out more explicitly. The general algorithm is that we build number n + 1 by joining the preceding set n and a copy of n embedded in a new set. The set-joining operation is known as union (∪), so we can formalize a Peano-like successor function for ordinals as:

\(S(n) = n ∪ \{n\}\)

To infinity… and beyond

Almost all mathematicians accept the existence of infinite sets; a common example would be the set of all natural numbers, ℕ. Every natural number itself is finite, but there is no upper limit on how large these numbers can get; whenever you pick some n, I can always best you by shouting “n + 1”.

The ordered set of all natural numbers looks like the product of our method for constructing cardinals — that is, if we allowed the process to continue without end:

\(\mathbb{N} = \{0, 1, 2, 3, 4, ...\}\)

It’s tempting to ask if the set can function as an infinite ordinal — i.e., an infinite number — and if yes, what numerical properties does it have?

Well, we can say right off the bat that the ordinal we’re talking about wouldn’t be a member of ℕ: every element of ℕ is finite. By extension, we can conclude that the ordinal must not be a successor to any natural number: if n is a member of ℕ, then so is n + 1, so the presence of a successor relationship would lead to the same contradiction.

Can such an unmoored, infinite ordinal exist? Well, that’s up to us to decide: conjuring it doesn’t lead to any outright paradoxes and opens up some weird but occasionally useful math.

We can name this ordinal ω; again, its set-theoretic representation is just:

\(\omega = \{0, 1, 2, 3, 4, ...\} = \mathbb{N}\)

Of course, inventing a symbol isn’t much of an accomplishment; the big question is whether, under the axioms of set theory, we can derive any useful arithmetic for this mysterious entity.

In school, you might have been exposed to notation along the lines of:

\(\infty + 1 = \infty\)

In an earlier article, I quipped that this notation is just a glorified calculator error message — all it tells us is that the result is too large for reals:

\(\texttt{<Error>} + 1 = \texttt{<Error>}\)

That said, if you’re accustomed to this way of thinking about infinity, it’s tempting to assume that the rule should apply to actual infinite numbers — i.e. that ω should be the same as ω + 1. Let’s test that hypothesis.

In line with the Peano rules, we can express ω + 1 as the application of the ordinal successor operation to the first operand. As a reminder, the successor operation takes the original infinite set of natural numbers (ω = ℕ) and then embeds that set as a new element to construct the next ordinal. We get:

\(\omega + 1 = S(\omega) = \omega \cup \{\omega\} = \{ 0, 1, 2, 3, 4, ..., \omega \}\)

We have previously established that ω itself cannot be a member of ℕ, because that would make it a natural number, and therefore, a finite quantity. Yet, the newly-constructed set corresponding to ω + 1 evidently does contain that element; this tells us that the set is categorically different from ℕ. We must conclude that ω ≠ ω + 1. More specifically, because ω + 1 contains ω, it sits higher in the rank of ordinals, a relationship we can write as ω < ω + 1.

But lest we get too cozy with this new reality: addition involving infinite ordinals is not necessarily commutative! To illustrate, let’s construct the set representing 1 + ω. As before, we rewrite addition as a (repeated) application of the successor function to the first operand:

\(1 + \omega = \underbrace{...S(S(S(1)))}_{\textrm{repeats } \omega \textrm{ times}}\)

Recall that we defined the ordinal 1 as a single-element set containing zero: {0}. Starting from that set and applying the successor function, we end up constructing ordinal 2 — another name for {0, 1}. The next application of the nets us 3, aka {0, 1, 2}:

\(\begin{align} 1 &= \{0\} \\ S(1) &= \{0, 1\} \\ S(S(1)) &= \{0, 1, 2\} \\ ... \end{align}\)

If we repeat this operation ω times, we obtain an infinite set { 0, 1, 2, 3, 4, … }. Note that the element ω itself can never make it into the set: it’s not a successor of any natural number, so it can’t be reached by repeatedly incrementing one.

Upon closer inspection, the resulting 1 + ω set is indistinguishable from the set of natural numbers, ℕ. We know that ω is also just another name for ℕ, so we can write the following equality: 1 + ω = ω. Few paragraphs earlier, we showed that ω < ω + 1. This leads to a surprising result: 1 + ω < ω + 1.

One might ask if non-commutative addition is a violation of one of the axioms of standard arithmetic. It isn’t, on a technicality: the rules apply only to finite numbers, such as the members of ℕ. Luckily for us, ω isn’t invited to that club.

Before we wrap up, let’s have a look at another interesting corner case: ω + ω (aka ω · 2). To calculate this ordinal, we start with ω = { 0, 1, 2, 3, 4, … } and then iteratively extend the set through the successor operation. We first append ω, then ω + 1, then ω + 2, and so on:

\(\omega \cdot 2 = \{ 0, 1, 2, 3, 4, ..., \omega, \omega + 1, \omega + 2, ... \}\)

The tail end of this ordered set is an infinite sequence of successors to ω; as in all the earlier cases, ω · 2 can’t be a member of itself, so ω · 2 must not be reachable by incrementing ω. This is analogous to how ω couldn’t be reached by incrementing any finite number; the discontinuity repeats for each multiple of ω.

Cardinal sins

It’s tempting to say that each of our set-theoretic numbers describes the element count of the underlying set:

\(\newcommand\explainabove[2]{% \overset{\overset{\textnormal{#1}}{\downarrow}}{#2\mathstrut}} 5 = \{\explainabove{1}{0}, \explainabove{2}{1}, \explainabove{3}{2}, \explainabove{4}{3}, \explainabove{5}{4}\} \)

Yet, in the realm of the infinite, this statement is suspect. If we start counting elements from one, we can never get to ω or above because there’s no successor relationship between counting numbers and infinite ordinals. By this method, the size of any infinite set appears to be incalculable.

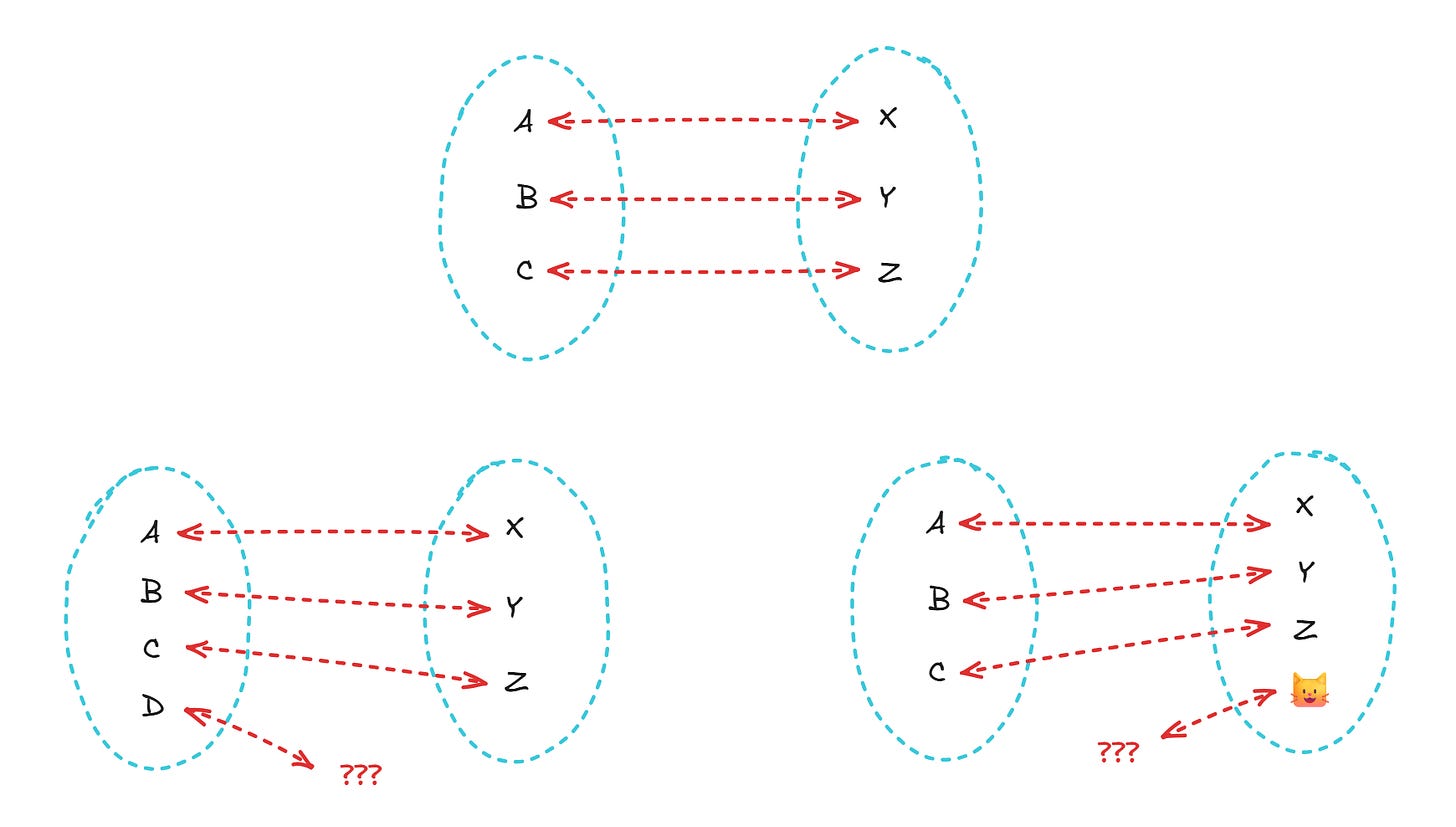
Luckily, there are several ways to reason about set sizes without resorting to a tally. The simplest approach is to declare that set A is smaller than B if A is a strict subset of B. For example, we may assert that { 🐱, 🥔} is smaller than { 🐱, 🥔, 🐸}.

We could also consider two sets to be of equivalent “magnitude” if we can map their elements one-to-one. It doesn’t matter which element gets mapped to which, as long as there are no orphaned members on either side:

One equivalent pair (top) and two non-equivalent ones (bottom).

This particular measure of equivalency on the basis of a one-to-one mapping is called cardinality.

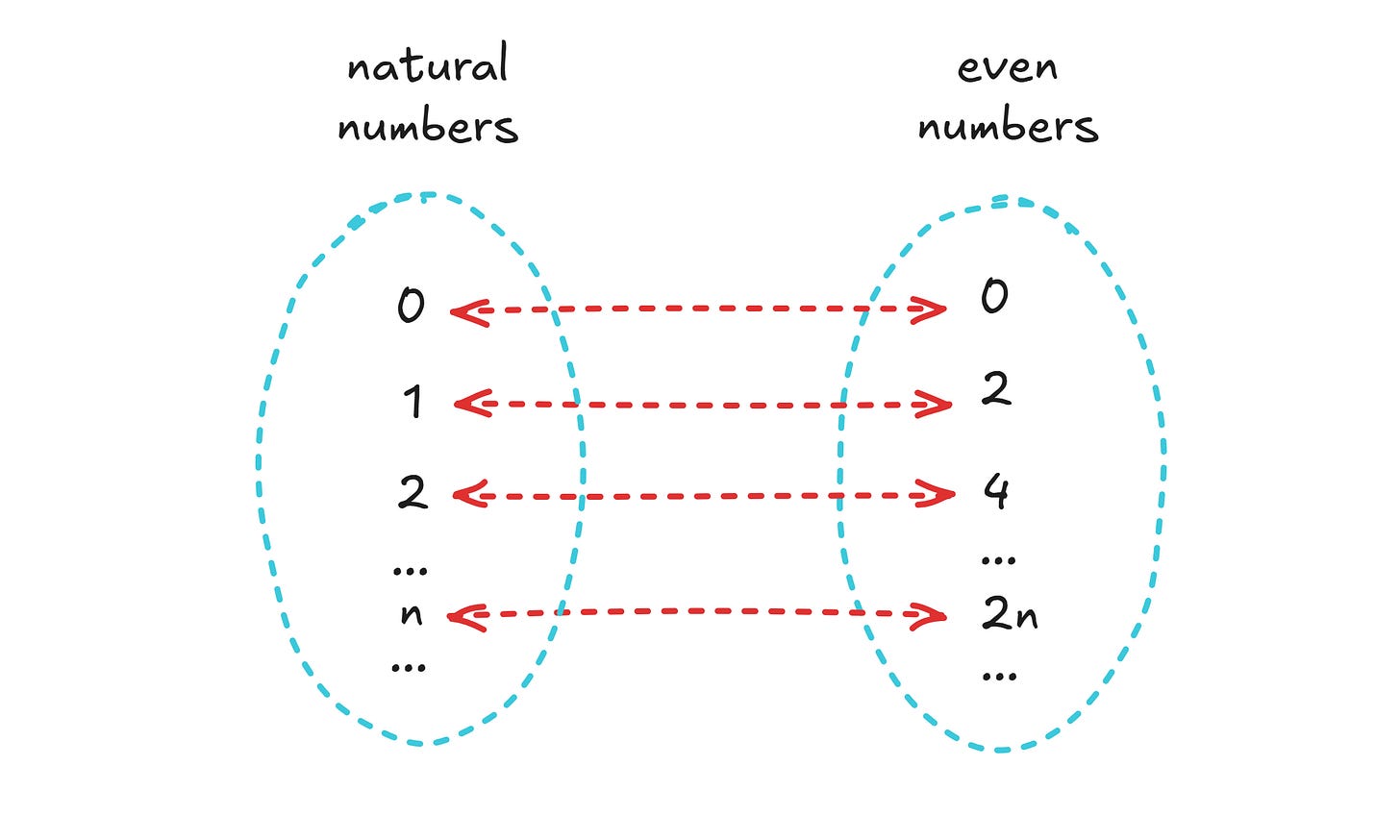
The concepts are dead simple for finite sets, but consider a set of natural numbers next to a set of every even number (E). Obviously, E is strict subset of natural numbers, so by our first rule, we ought to say that E is smaller than ℕ. Yet, if we’re talking about a one-to-one mapping for a pair of infinite sets, the following approach is perfectly fine:

This is legal in 47 states.

The sets are infinite but only contain finite numbers. For any finite n picked from ℕ, n multiplied by two is also finite and therefore can be found in E. We say that the set of natural numbers has a specific cardinality — aleph-null, ℵ₀ — and that the cardinality of the set of even numbers is the same.

Do any other infinite cardinalities exist? The answer, as demonstrated by Georg Cantor, appears to be yes! Imagine some arbitrary one-to-one mapping from every single natural number to reals (ℝ), e.g.:

\(\begin{array}{c} 1 & \rightarrow & 0.\underline{\textbf{1}}23456... \\ 2 & \rightarrow & 0.6\underline{\textbf{5}}4321... \\ 3 & \rightarrow & 0.99\underline{\textbf{9}}999... \\ 4 & \rightarrow & 0.454\underline{\textbf{5}}45... \\ 5 & \rightarrow & 0.1111\underline{\textbf{1}}1... \\ 6 & \rightarrow & 0.03133\underline{\textbf{7}}... \\ & ... & \end{array}\)

There’s nothing special about these values; the only point is that we have a distinct real number assigned to every member of ℕ. There are obviously at least as many reals as there are natural numbers, so this is something we should be able to do.

The remaining question is whether there are any orphaned reals left once all the natural numbers are used up. To figure this out, let’s try to construct a new real number, d. We start by looking at the first row above:

\(1 \rightarrow 0.\underline{\textbf{1}}23456... \)

We take the underlined (first) decimal digit of the real and then choose any value other than this one for the corresponding digit in d. In this case, the offending digit is 1, so we can pick 0, 2, 3, 4, 5, 6, 7, 8, or 9. Let’s go with 9:

\(d = 0.\textbf{9} \textrm{ (...to be continued)}\)

We then proceed to the second row, this time looking at at the second decimal digit — essentially, following the diagonal pattern underlined in the assignment diagram. Once again, for the second decimal digit of d, we choose any value other than the actual digit marked in row 2; since the highlighted value is 5, we can pick 2 instead:

\(d = 0.9\textbf{2} \textrm{ (...more to come)}\)

In row three, we can replace 9 with 0; in row four, let’s substitute 5 with 4. For row five, we trade 1 for 3; in row six, we use 5 instead of 7. We keep following the diagonal pattern to infinity:

\(d = 0.920435...\)

What’s special about this result? Well, by construction, d differs by at least one digit from every single real number in our mapping! For example, it can never match row 1 because the first decimal digit is 9 instead of 1; it also doesn’t match row 2 because the second decimal digit is 2 instead of 5.

That is to say, d can’t possibly appear anywhere on the list that assigned a real to every integer. Thus, we have found an orphaned member of ℝ; the cardinality of natural numbers (ℵ₀) is evidently less than the cardinality of reals (also known as the cardinality of the continuum).

Cantor’s argument is often treated with suspicion by folks who are accustomed to there being only one kind of infinity. That said, as we’ve shown earlier on, if you accept the notion of infinite sets, you necessarily end up with a hierarchy of different ordinal infinities. Cantor’s cardinalities are just a cherry on top.

Are there any cardinalities in between ℕ and ℝ? Mathematicians don’t think so, but this hypothesis is provably undecidable within the traditional axioms of set theory.

Is any of this real?

Maybe? If infinity lurks in some dark corners of the physical universe, we probably have no way of ascertaining its numerical properties. In the absence of this, we have a toolkit for creating weird worlds that restate the rules of formal logic in increasingly mind-bending ways — and sometimes help prove a theorem or two.

Because the behavior of infinite sets is bizarre, there is a school of mathematics that rejects their existence. Heck, there is a small number of mathematicians who reject infinity altogether. The difficulty is that such decisions require discarding vast amounts of useful math — or at the very least, tossing out an explanation of why we’re doing that math in a particular way.

On some level, this might not be a big deal: calculus is usually still taught without providing a rigorous justification for limits or infinitesimals. On the flip side, as almost any calculus student will attest, it’s an intellectually unsatisfying approach.

Just as important, without all these wonderfully confusing notions of infinity, how do you keep the riff-raff out of math?

👉 Reader exclusive: for an essential Peano arithmetic calculator, click here.

---

If you’re interested in beavers in addition to turtles, you’re probably going to enjoy this article. And if you like the content, please subscribe; there’s no better way to stay in touch with the writers you like.