Real MLCCs (and inductors) have curves

Linear components are pretty nonlinear -- and parasitics don't tell the whole story.

This article assumes some familiarity with capacitors and inductors. If you need a refresher, check out this write-up first.

Most folks who dabble in electronics know that electrolytic capacitors are messy: they have non-trivial internal resistance and leakage currents, they age over time, and they tend to explode if you accidentally reverse polarity.

In contrast, multilayer ceramic capacitors (MLCCs) appear pretty close to the textbook ideal of a capacitor. They have negligible resistance, negligible leakage currents, and only a tiny bit of inductance that doesn’t really get in the way of most hobby designs.

Sure, you might have heard that common MLCCs lose capacitance at extreme temperatures. That said, the effect is fairly minor between 0 and 40 °C (32 - 104 °F) — so outside of automotive applications, there’s little to worry about.

More cryptically, it’s sometimes asserted that MLCCs lose capacitance “under DC bias” — that is, you get lower capacitance if you have a sine signal centered around 5 V than if it’s centered around 0 V. That seems harmless — but it’s also a pretty serious understatement of what’s actually going on.

The truth about MLCCs

Fundamentally, an ideal capacitor is a device that allows a certain amount of charge (Q) to be stored in an internal electric field with the application of a certain electromotive force. Capacitance (C) measures the relation between the voltage and the stored charge; the less force is needed to move a certain number of electrons onto the plates, the higher the capacitance:

\(C = {Q \over V}\)

The flow of one unit of charge per second is defined as one ampere. It follows that if we’re charging a capacitor with a constant current I for t seconds, the voltage across the terminals will be given by a simple linear formula:

\(V_{cap} = {I \cdot t \over C}\)

In other words, if we’re repeatedly charging and discharging a capacitor with constant current, we’d expect to see the voltage to ramp up and down in a linear fashion, producing a triangle waveform.

Let’s try that for an electrolytic capacitor, and then for a beefy MLCC; both capacitors are rated for 10 V. I believe the MLCC in question is Murata GRM31CR61A107MEA8K, although I didn’t save the label when I put it in the parts bin:

Constant-current charging of a 100 µF capacitor. Measured by author.

Huh?

To maximize their capacitance, many MLCCs use ceramic materials that exhibit a property known as ferroelectricity; such materials contain permanent electric dipoles that are easily, elastically reoriented with the application of an external field. This allows for the storage of far more energy compared to a dielectric devoid of permanent dipoles. That said, the number of dipoles in the material is limited, and their response is the strongest when the field is just starting to ramp up. Once most of the dipoles are oriented along the field — which evidently happens somewhere around 2.5 V — the capacitor stops working nearly as well. Less charge is needed to produce the same increase in voltage, which manifests as a spike in the bottom plot.

The phenomenon is specific to type II and type III dielectrics; common product codes in this category include Z5U, Y5V, X5R, and X7R. Type I dielectrics (C0G, etc) do not have this problem because they’re not ferroelectric; that said, these ceramics also have a markedly lower attainable capacitance for the same component size.

The effect is more profound than usually implied; it’s signal distortion, not just a quirk related to “DC bias”. Any voltage that’s getting even remotely close the component’s rated limit is bad news.

To be fair, the phenomenon is not worth modeling with any real zeal; instead, we can either “upsize” the capacitance to have a comfortable safety margin in applications where the value isn’t critical (e.g., IC decoupling); or we can choose an MLCC rated for a higher voltage or made out of a class I ceramic.

Inductors do that too!

An inductor is essentially an “inside out” version of a capacitor, in the sense that the relationship between current and voltage is flipped around. The component develops a voltage across its terminals that is proportional to the step change in applied current; for a capacitor, it’s the current that follows the step change in voltage.

If we’re applying a voltage-based square wave signal to an inductor, the current should be ramping up and down linearly, resembling a triangle wave. That’s indeed what happens — but only up to a point:

Inductor response to a square wave. Measured by author.

In the second scenario, the frequency of the square wave is lower, so the current ramps up to a higher value. As it turns out, once it crosses around 300 mA, the inductor suddenly becomes a nonlinear device.

Once again, the mechanism is similar: the core of an inductor is a ferromagnetic material with a number of microscopic magnetic domains. These domains are reoriented in response to the field generated by the current flowing through the inductor’s winding. The number of the domains is finite and the bulk of the reorientation happens not far from the crossover point. Once we exceed a certain field strength, the core more or less turns into a paperweight.

Because of this, most inductors have two current limits specified. One is the absolute safety limit dictated by the component’s ability to dissipate heat; the other is a consequence of the saturation characteristics of the core. Many small inductors are designed to keep both values roughly the same, but it’s not a universal rule.

This is also a big part of why transformers designed to work at low frequencies are physically larger. To deliver the same amount of power to the secondary winding while operating at a lower frequency, the current in the primary winding must ramp up to a higher value in every cycle. Not only does this call for bulkier conductors, but the core needs to be beefed up too. Before the advent of high-frequency switching power supplies, most AC adapters could double as formidable home defense weapons.

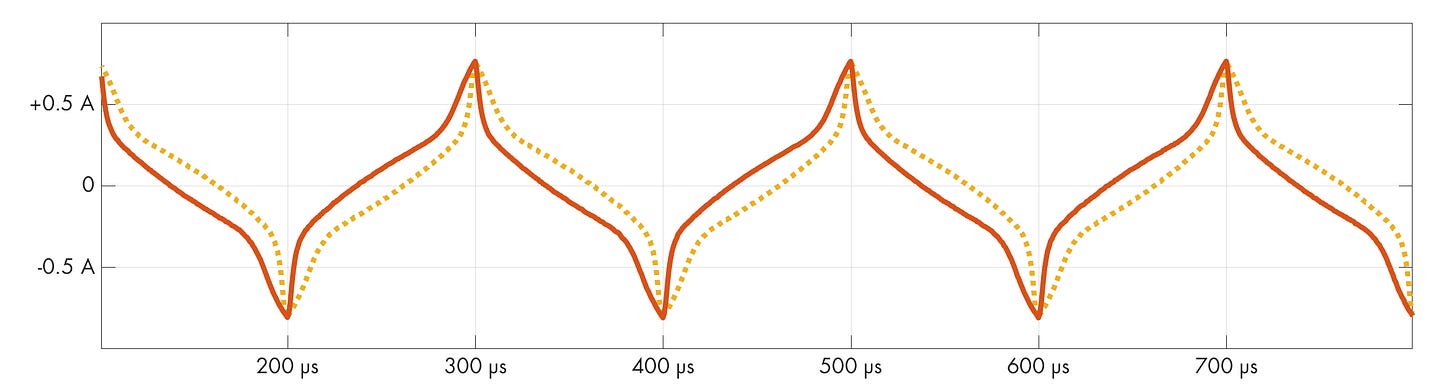
Since we’re on the topic of nonlinear behaviors, another interesting observation about the inductor figure is that the bottom plot of current is not quite symmetric; the ramp down is not a mirror reflection of the ramp up. The following plot shows the asymmetry:

Measured current (red) versus a mirror image (dashed orange).

This happens because the response of magnetic dipoles isn’t as good as for the electric dipoles in a capacitor; instead of bouncing back elastically, some remain in a magnetized state. It takes energy to rotate them back and forth, but that energy is never returned to the circuit. This phenomenon, known as magnetic hysteresis, is a significant cause of losses in the core.

👉 For a discussion of capacitors in the context of signal filtering, see here. For modeling thermal noise in electronic circuits, click here. A catalog of other articles on electronics can be found here.

---

I write well-researched, original articles about geek culture, electronic circuit design, and more. If you like the content, please subscribe. It’s increasingly difficult to stay in touch with readers via social media; my typical post on X is shown to less than 5% of my followers and gets a ~0.2% clickthrough rate.