Deep dive: the (in)stability of op-amps
A closer look at op-amp feedback loops and the stability criteria for circuits that use them.
This article assumes some familiarity with signal amplification and the knowledge of basic op-amp circuits. If you need a refresher, start here.
In a recent write-up on photodiodes, I mentioned that adding a capacitance in an op-amp’s feedback loop can spell trouble: it might cause ringing, sustained oscillations, or excessive gain.
It’s easy to offer a hand-wavy explanation of this phenomenon, but the mechanics of amplifier feedback loops are worth a closer look: control feedback is ubiquitous in analog signal processing and can be tricky to get right. Alas, the underlying theory is rather inaccessible to hobbyists; you’re either getting sucked into the discussion of zeroes and poles of complex-number transfer functions, or into obtuse jargon along the lines of this snippet from Analog Devices:
"The amplifier’s stability in a circuit is determined by the noise gain, not the signal gain."
What does noise have to do with stability? Not much! If you’re curious, the term has to do with the habit of modeling real-world op-amps as an ideal amplifier with a voltage noise source attached to one of its legs. For some reason, Texas Instruments insists it has to be the non-inverting leg:
“Input voltage noise is always represented by a voltage source in series with the noninverting input.”
So… is “noise gain” just a trade term amplification on that leg? Do op-amps have different gains on each input? How do you set this gain, or where do you find it in the spec?…
All these abstractions make sense in the context of mathematical models, but they don’t build intuition about the real world. In today’s article, let’s talk about feedback loops in a more accessible way. We’ll get to the same results, but hopefully in a less confusing way.
Back to the basics: the open-loop amplifier
Before we proceed, let’s revisit the following rudimentary op-amp circuit:
If you’re here, you should already know the basic behavior of an op-amp: it takes the difference between the two input voltages, amplifies that by some very large number (open-loop gain, AOL), and then outputs the amplified difference as another voltage. Strictly speaking, the output is typically referenced to the midpoint between the power supply rails — let’s call it Vmid — so the complete formula is:
This is the only thing the chip does. Despite the confusing terminology we use to describe op-amp circuits, the IC never pays attention to absolute input voltages, and it can’t be configured to have any other gain.
Because AOL is normally huge — 100,000 or more — there’s just a microvolt-range linear region around Vin+ ≈ Vin-. Any input difference larger than that is bound to send the output all the way toward one of the supply rails. We can trivially simulate the behavior of the aforementioned circuit, keeping in mind that Vin- is permanently tied to 2.5 V:
In effect, the op-amp is a voltage comparator: the circuit outputs 0 V when Vin+ drops below 2.5 V, or 5 V when it’s above.
For completeness, we should note that there is an important caveat to this model of an op-amp: the capacitances, inductances, and resistances inside any real-world IC limit the chip’s response speed. To avoid issues, the designers usually engineer the op-amp so that AOL gracefully rolls off past a certain point, halving with every doubling of the frequency of an input sine wave. It eventually reaches 1x (unity gain) — and past that point, you’re stuck with an attenuator instead of an amplifier:
(Some readers might recognize that this is the curve of a first-order RC lowpass filter — as discussed in one of the earlier articles.)
The voltage follower
In practice, op-amps are typically employed with some form of a negative feedback loop. The simplest example — a voltage follower with an apparent 1x (unity) gain — is shown below:
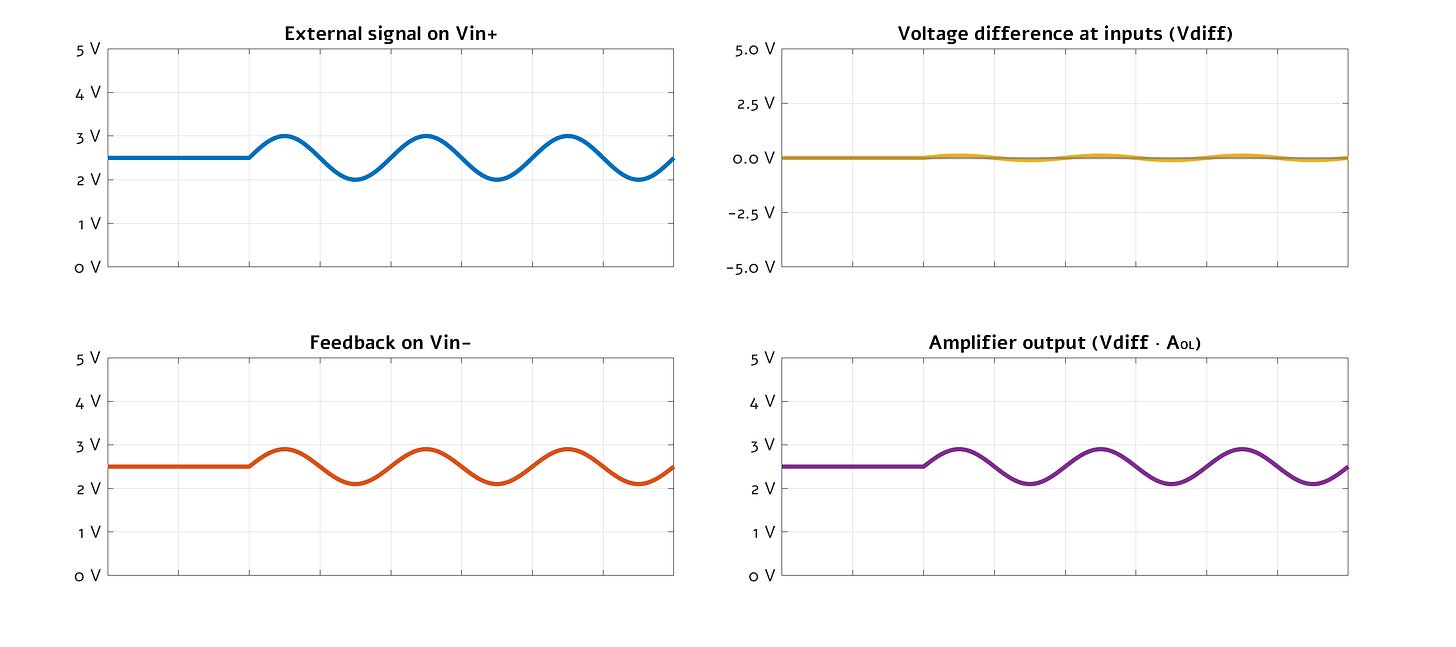
At a glance, the circuit seems trivial. The output voltage is looped back onto the inverting input, so if Vin+ > Vout, the differential signal is positive and the output starts creeping up; conversely if Vin+ < Vout, the voltage starts moving down. The process stops once the circuit reaches an equilibrium between all three voltages — essentially forcing Vout to march in the lockstep with the input signal on the Vin+ leg:
Except, this explanation is not quite right. We often take the mental shortcut of assuming that the circuit’s equilibrium is reached at Vin+ = Vin- = Vout — but that’s not actually possible. Remember that at its core, the op-amp is doing the following math:
If the differential voltage is zero, then Vout is constant, no matter the value of AOL. But if Vout (and by extension, Vin-) are stuck in place, then not only is the circuit not doing anything useful, but the differential voltage couldn’t actually be zero. Oops!
What happens in reality that a steady state is reached with Vin- and Vout at a slight offset from the Vin+ input signal. This “error”, when multiplied by AOL, is just enough to produce the correct output voltage. The presence of a negative feedback loop means that any deviations from the stable equilibrium are swiftly countered.
We can figure out the exact magnitude of the offset if we take the op-amp equation and just substitute Vin- with Vout. The substitution just gets rid of an extra variable — and is fair game because in the follower circuit, the two pins are tied together:
The analysis partly vindicates the mental shortcut we have talked about before: when AOL is very high, it follows that 1 / (1 + AOL) ≈ 0 and AOL / (1 + AOL) ≈ 1, so the last expression is kinda-sorta equivalent to:
That said, although the scale of the error nudges is often negligible, ignoring the phenomenon makes the behavior of op-amps difficult to grasp: after all, the nudges are the only thing that is getting amplified!
Just as importantly, as the input signal frequency increases, the op-amp’s internal gain drops, so Vout must drift farther away from the target for the sufficient differential voltage to appear across the input pins. In other words, at high frequencies, the output voltage error caused by feedback can get quite high.
The non-inverting voltage amplifier
Next, let’s look at the usual way of adding gain to a voltage follower:
The operating principle of this circuit is simple: the resistors reduce the voltage on Vin- by a factor of two — so for the input signals to get in the same vicinity, the output voltage has to swing to Vin+ * 2.
The gain configured by the resistors cuts into the op-amp’s AOL, but not for the reason we usually assume. All we’re doing is using some external circuitry to prompt the op-amp to output a different voltage; what does it matter if we’re asking for Vin+ multiplied by 0.5, 7, or -2? The AOL value is a constraint on differential gain, not on the relation between Vout and Vin+. Signal gain is free! The chip don’t care!
The problem lies elsewhere: the resistors attenuate the nudges that piggyback on top of the output signal. It used to be that Vin+ and Vout needed to differ only by some small amount to encode a full range of input voltages; let’s call that difference Vdiff. Now, because of the added attenuation, we need Vdiff * 2 to achieve the same result. This is akin to replacing the op-amp with a chip that has half the AOL we started with. If we push the configured amplification far enough, the effective AOL drops below 1, and for the circuit to work, Vdiff would need to be impossibly high.
This might seem like an academic distinction, but there are less common op-amp circuits where signal amplification is done differently does not come at the expense of AOL.
Understanding loop gain
As should be clear by now, the feedback loop doesn’t actually change the op-amp’s gain. All we’re doing is offsetting Vin+ from Vin- in a specific way. In the closed-loop configuration, the chip’s internal amplification remains very high — and for the sake of signal accuracy, we want it to stay that way!
In a way, the feedback nudges can be thought of having their own gain, separate from any signal amplification configured by the designer of the circuit. In the case of a voltage follower, the configured signal gain is 1x, while the amplification of the feedback “error” is many orders of magnitude higher.
For the standard voltage amplifier topology, the magnitude of this loop gain is proportional to the vertical distance between the op-amp’s intrinsic amplification curve and the circuit’s configured voltage gain (in our example, 1x):
It’s worth noting that the closed-loop gain curve is not always flat; in particular, with feedback-path capacitances, it might start climbing or rolling off at some high frequency. Some exotic op-amps might also have kinks in the AOL curve. That said, for the sake of simplicity, let’s assume that none of that is going on.
At this point, we have a preliminary explanation of one of the more counterintuitive properties of op-amps: that instability and some types of noise problems can get worse at lower signal amplification rates. The higher the gain in the feedback loop, the more pronounced are the consequences of any signal errors introduced along that path.
The tape-delay op-amp circuit
This brings us to the following unorthodox design:
It’s a voltage follower — except for a contraption that records output voltages and plays them back some time later on the Vin- side, delaying the feedback signal by a preset amount. A temporal defect in the loop!
To explore this circuit, I built a toy discrete-time model with a limited bandwidth and a feedback loop that lags by five “ticks”. I then supplied a single input pulse on Vin+ and let the simulation run:
For the first five ticks, Vin+ (blue) is seeing a positive pulse while Vin- (red) is staying put due to the delay. As a consequence, Vout shoots up — although because of the baked-in bandwidth limit, it does not immediately jump all the way to +5 V.
After five ticks, Vin+ goes back to the mid-point and stays there for the rest of the simulation — but all of sudden, the delayed echo of the last pulse arrives on Vin-. It pulls the differential voltage negative, thus producing an inverted echo on the output. This back-and-forth process continues for a while, with gradually decaying amplitude.
The most important observation is that past the initial stimulus, the entire action is contained to the feedback loop. There is no movement on the signal input (Vin+), so the configured signal gain plays no role. The only reason the oscillations decay over time is that at the offending “echo” frequency, the gain of the feedback loop itself happened to be a tad below one.
If we increase loop gain a tiny bit, we get this result:
In the end, there are two conditions that must be met for sustained oscillation:
There must be a feedback delay of about one-half of a wavelength (180°) at some sine-wave frequency.
The feedback loop gain at that frequency must be at least one.
The first requirement means that higher frequencies are of more concern, because it’s easier to accidentally introduce comparatively large delays when the wavelength you’re working with is short. The second requirement means that we generally only have to worry about the frequencies below the IC’s internal unity-gain point.
But what kind of a weird contraption is that?!
Right. Tape-delay mechanisms are not commonly employed in op-amp circuits. Non-negligible transmission delays can sometimes crop up in electronic designs, but feedback loops are usually pretty compact on any sensibly-designed PCB. Unless you’re working with ultra-high frequencies or very long wires, signal propagation times are a relatively remote concern.
Yet, there is another, more ubiquitous form of a “delay” mechanism: the capacitor. To be clear, a capacitor is not really a time delay device: it can’t store and replay past waveforms. Instead, it’s an integrator — that is, its terminal voltage is a function of the charging currents that flowed through it before. It might sound math-y, but it’s akin to how a bucket in your backyard “integrates” rainfall over time, “outputting” the result as a water level you can observe.
Integration distorts most waveforms — but in the special case of a sine, it just produces a phase shift:
The phase shift is between the charging current and the output voltage. Current measurements are not commonly used for conveying data in electronic circuits, but if the capacitor is charged and discharged through a resistor, the amps that flow through the resistor are proportional to the applied voltage — so we get some degree of voltage-to-voltage shift, too. A detailed discussion of this phenomenon can be found in an earlier article on RC filters, so I won’t repeat it here — but in essence, the resistor-capacitor circuit adds from ~0° to ~90° phase shift, depending on R and C values and signal frequency.
This phenomenon can be observed when shunt capacitances are added to op-amp feedback loops, even without any discrete resistors. That’s because the amplifier’s output transistors have some non-zero impedance (ZO or RO in the spec). The number often hovers around 20 to 100 Ω, and it acts like a hidden series resistor in the output path.
On the surface of it, even the worst-case RC filter shift (~90°) is nowhere near the ~180° offset needed for sustained oscillation — but op-amps have some internal phase shifts too. The devices are usually designed so that their bandwidth rolls off just ahead of the danger zone, leaving just a bit of phase margin for external components. With some ICs, even as little as an extra -45° can be enough to put you in the red.
When that happens, short of reducing the capacitance, some of the hacks may involve reducing the bandwidth of the feedback loop; bumping up signal gain; or switching to an amplifier that has more of a phase margin at the frequencies of concern.
If you liked this article, please subscribe! Unlike most other social media, Substack is not a walled garden and not an addictive doomscrolling experience. It’s just a way to stay in touch with the writers you like.
For a thematic catalog of articles on electronics and other topics, click here.