The basics of signal amplification
The basics of signal amplification
Transistors and op-amps amplify signals - but what does it mean, exactly, and how to get it right?
As a computer geek, I never had much trouble navigating the world of microcontrollers and logic gates. Analog circuitry proved to be a different story; for a good while, I resigned myself to copying other people’s designs and going on wild-goose chases to procure long-obsolete parts that cropped up on the schematics.
After years of trial and error, I know that analog signal processing is a complex area of study — but I can finally navigate it with relative ease. In today’s article, I’d like to share some notes on one of the most common circuit design tasks: amplifying weak signals to make them suitable for driving analog-to-digital converters, speakers, LEDs, and other I/O.
(If you need a refresher on concepts such as voltage or resistance, start here.)
What is amplification, anyway?
There are two types of amplification circuits you are most likely to encounter: voltage and power amplifiers.
Voltage is straightforward. Voltage levels are the primary way of conveying information in electronic circuits, and every now and then, you end up with a signal amplitude that’s too microscopic for other devices to discern. An example might be the output of an electret microphone, a photodiode, or a temperature sensor — all firmly in the millivolt range. The job of a voltage amplifier is to multiply these small readings by some fixed value (“gain”), thus producing an output signal suitable for general use.
Power amplification is different. You might have come across signals that look good when measured in an open circuit, but that drop precipitously when connected to a load; a classic example is a microcontroller output pin interfaced directly to a motor or a speaker. The signal’s sudden attenuation is a straightforward consequence of Ohm’s law: V = IR. A single pin on an MCU can at best deliver around 40 mA; if it’s driving an 8 Ω speaker, the voltage across the speaker’s terminals will not exceed 320 mV (40 mA * 8 Ω), no matter what the chip is hoping to achieve. To get a 5 V difference across the speaker’s terminals, we’d need to pump out 625 mA.
A source that can’t supply appreciable currents is said to have high impedance. A power amplifier is a device that takes this high-impedance signal and then cranks out a low-impedance copy through a beefy output stage that can supply larger currents with ease. Unlike in a voltage amplifier, the input signal and its amplified version might look the same on an oscilloscope screen.
Conditioning signals for amplification
A near-universal constraint of amplifier circuits is that they can’t output voltages higher than the positive supply rail, or lower than the negative one. The output range is sometimes more constrained, but almost never extends beyond the supply.
It follows that if you have a signal that fluctuates between 1.0 and 1.05 V, you can’t simply amplify it by a factor of 100 in relation to the ground; that would put the output in the out-of-whack range of 100 to 105 volts. It can be similarly challenging to amplify any signal that extends below the negative supply rail, as some audio signals are liable to:
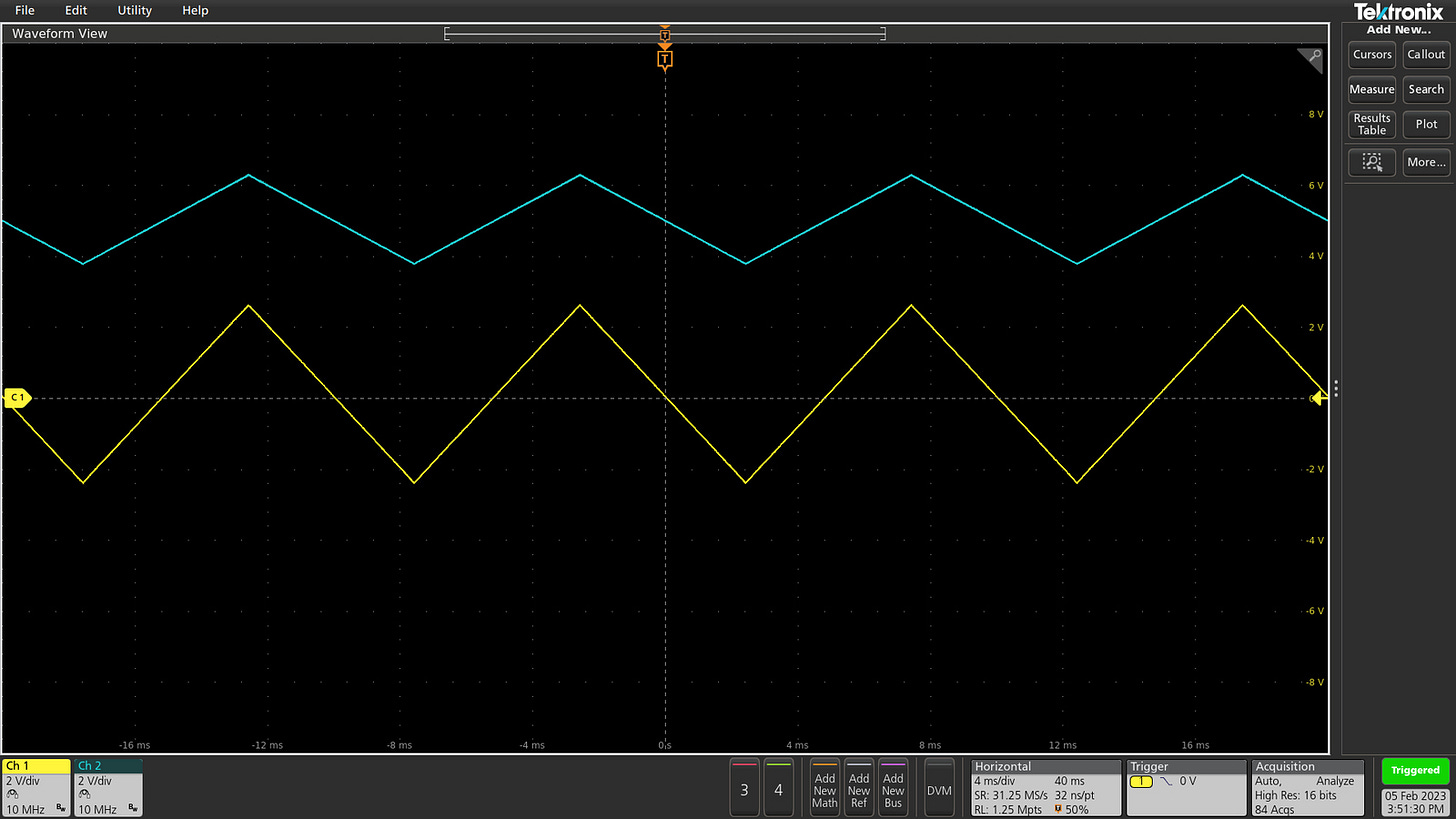
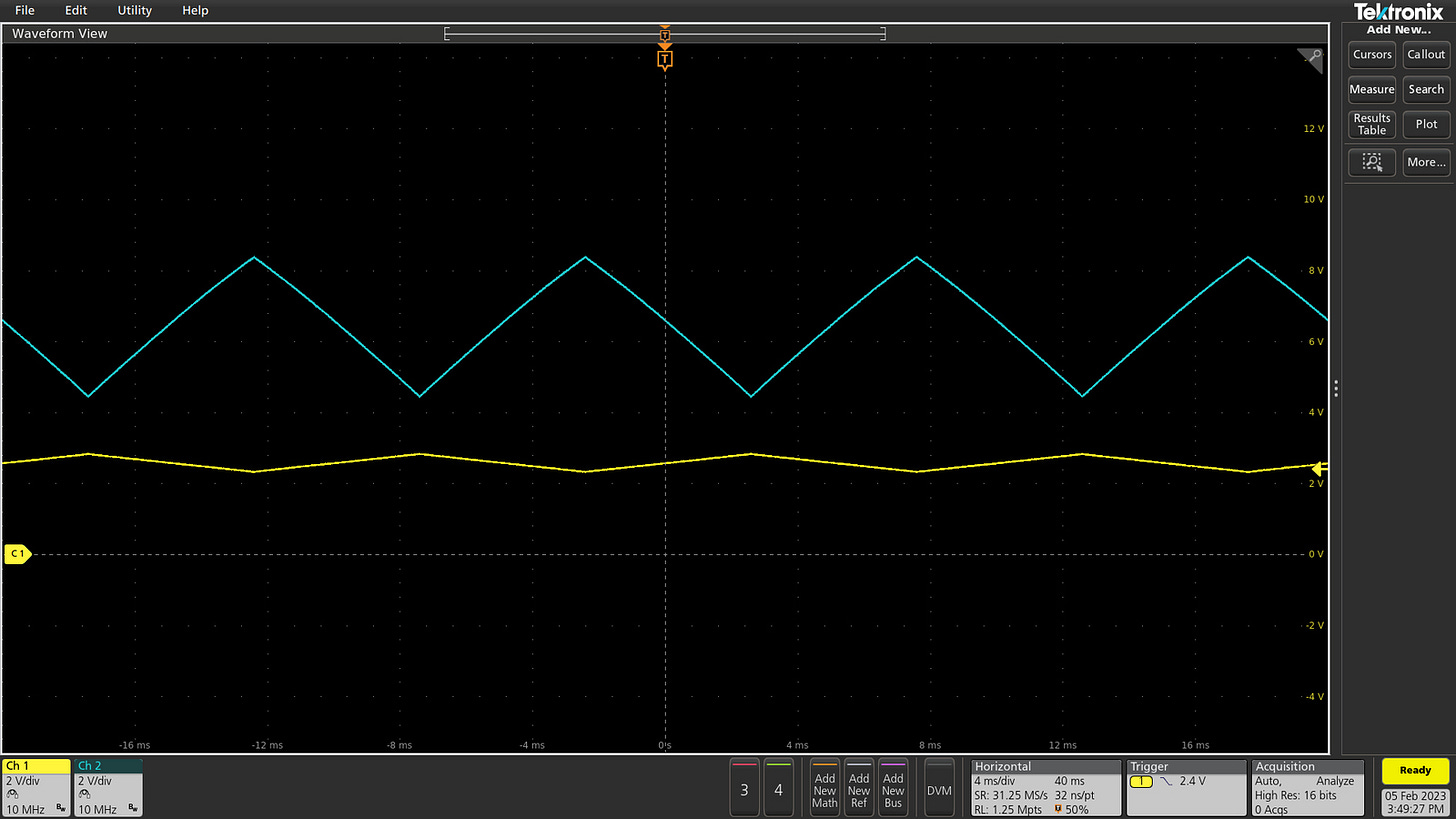
Short of building a second, wider-range voltage supply just for the amplifier, the most obvious solution is to offset the signal before amplification. Let’s go with an example of an input waveform centered at 0 V and exhibiting a peak-to-peak amplitude of 5 volts. We can use the following circuit to pull it up:
For the sake of this thought experiment, let’s use the same value of R1 and R2, perhaps 10 kΩ. In this case, the output should be a simple average, with 50% contributed via the R1 leg, and 50% contributed via R2. If so, one would expect the new signal center point to be (0 V + 10 V) / 2 = 5 V; and the new peak-to-peak amplitude to measure (5 V + 0 V) / 2 = 2.5 V.
A quick test with an oscilloscope confirms the calculations. The original signal is shown in yellow, while the offset version is in blue:
Other ratios are possible; had we used R1 = 10 kΩ and R2 = 33 kΩ, we’d have ended up with a center point at ~2.3 V and a peak-to-peak amplitude of ~3.8 V. The only practical constraint is that the input resistor — R1 — must be kept large enough to avoid loading the source to any appreciable extent.
The most obvious problem with this circuit is that although it succeeds at offsetting the signal, it inevitably reduces its amplitude. This can be compensated for by increasing amplifier gain down the line, but extra noise is the price to pay for such shenanigans.
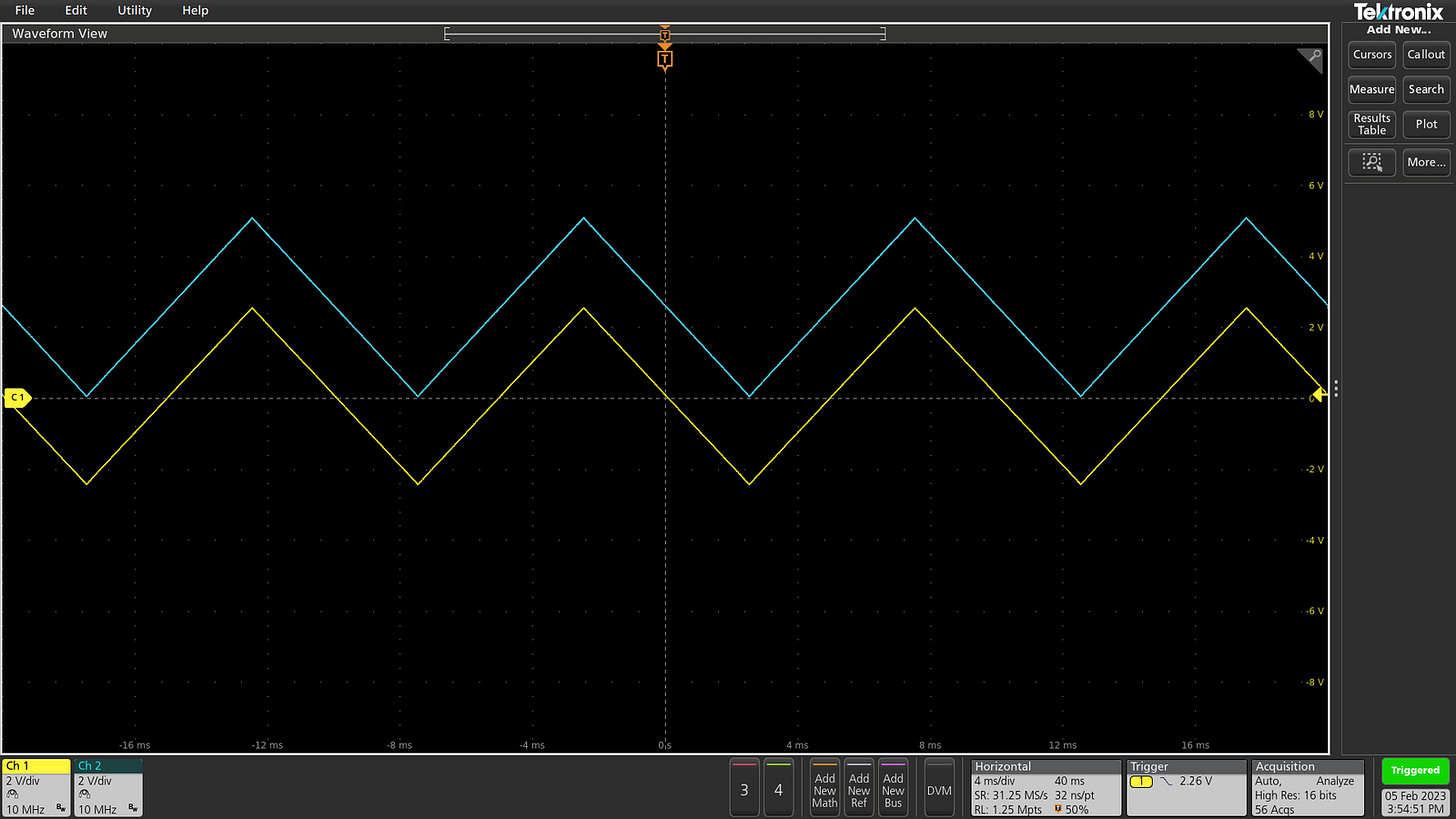
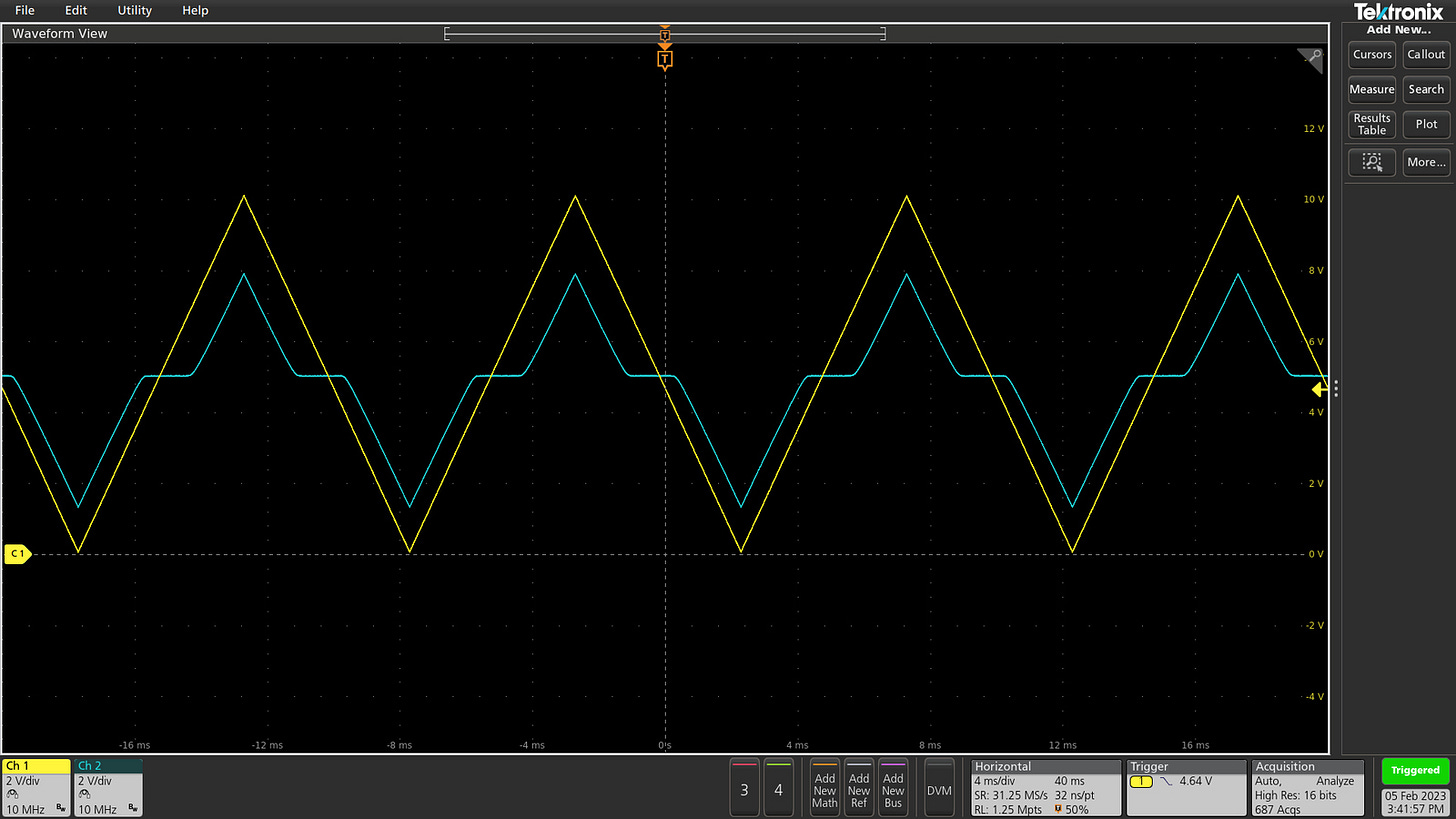
A more elegant solution is possible if we don’t care about preserving DC voltages, only about any higher-frequency AC signals that might be riding on top. This is common in audio circuits, and in this scenario, we can employ a DC-blocking capacitor in the signal path:
Because the capacitor doesn’t conduct DC, the output side is nominally free-floating in reference to the input, and the R1 and R2 resistors used to offset the output waveform can have a very high resistance — easily 100 kΩ or so.
Although DC voltages cannot pass, if the voltage on the input side suddenly jumps up or down, a proportional momentary voltage shift will be induced on the capacitor’s other terminal, where it can’t be immediately dissipated (due to the high values of R1 and R2). It follows that the circuit causes virtually no attenuation of AC signals at higher frequencies:
What are these “higher frequencies”? Well, assuming that there is no substantial output loading, the circuit’s frequency response characteristics are dictated chiefly by the RC highpass filter formed by C and the output-side resistors. If R1 = R2, the filter’s cutoff frequency is: f = ¼ × π × R1 × C.
As a practical example, with a 100 nF capacitor and two 100 kΩ output resistors, the the amplitude would start to roll off noticeably around 8 Hz.
Transistors as voltage amplifiers
This chapter assumes familiarity with the behavior of transistors, especially MOSFETs; if you need a refresher, please refer to this earlier article.
A transistor’s simplest use is as a switch. Let’s consider a common n-channel MOSFET in the following arrangement:
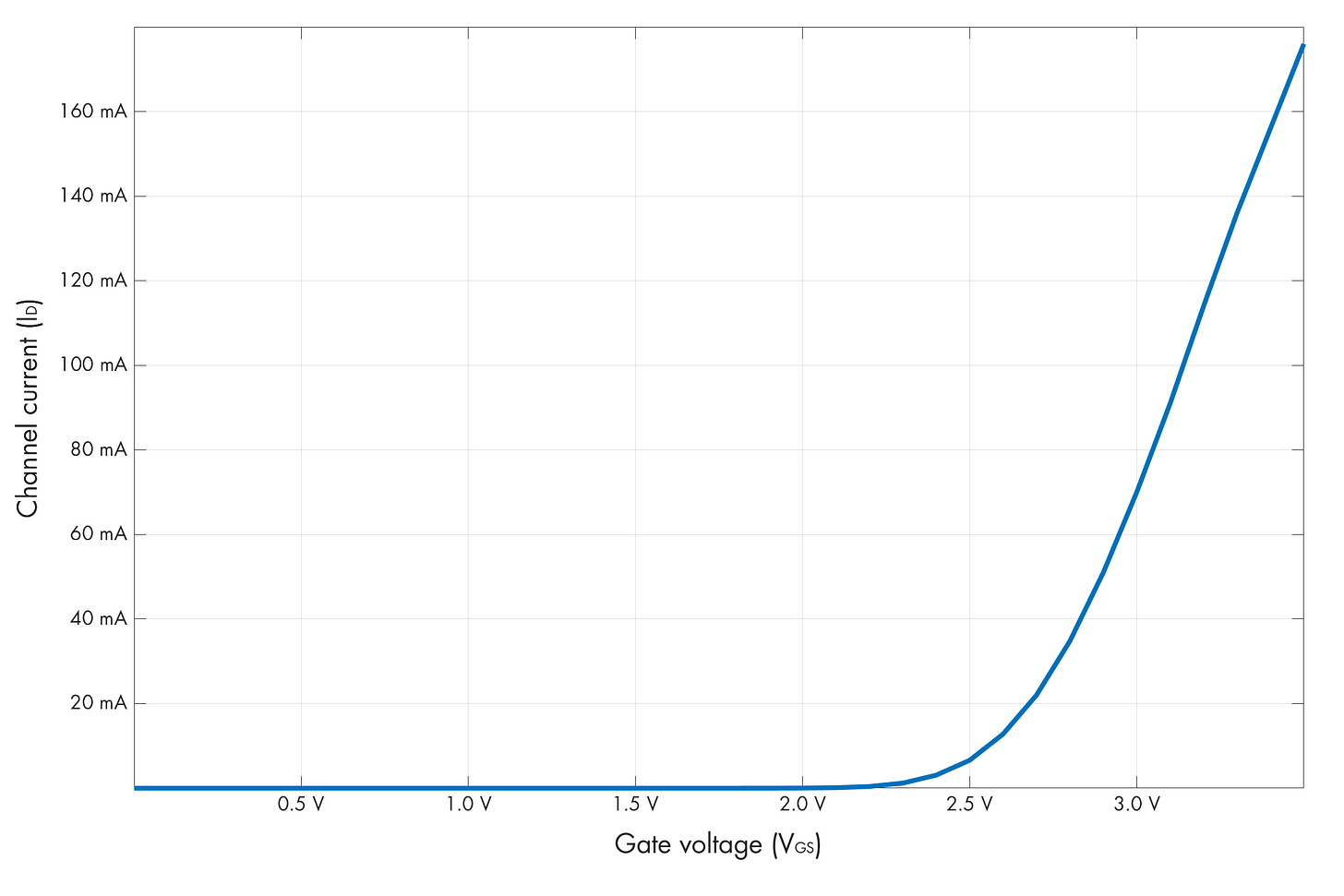
This transistor remains non-conductive until the voltage between its control terminal (gate) and its low-side terminal (source) exceeds the transistor’s intrinsic threshold voltage. The threshold voltage (Vth) usually hovers around 2 V, but varies from one transistor to another. Once Vgs clears Vth, the device starts conducting, and the load is energized.
There is a small linear region between “fully off” and “fully on”, and in this region, the transistor exhibits variable resistance proportional, among other things, to the applied gate voltage. Knowing this, many novices attempt to amplifiers by extending the switch topology, like so:
This is usually a mistake: the transistor’s voltage gain in that quasi-linear region is very high but unpredictable; it varies from batch to batch, and drifts due to factors other than Vth. To build a dependable amplifier, it is typically necessary to incorporate a feedback mechanism of some sort. A wider operating range would be nice too!
Building a voltage follower
Recall that an n-channel MOSFET conducts only when Vgs > Vth. In the previous example, we had the source terminal tied to the ground, so the Vgs differential was always equal to the magnitude of the input signal (Vsignal). But what if we allowed the source leg to drift away from 0 V?
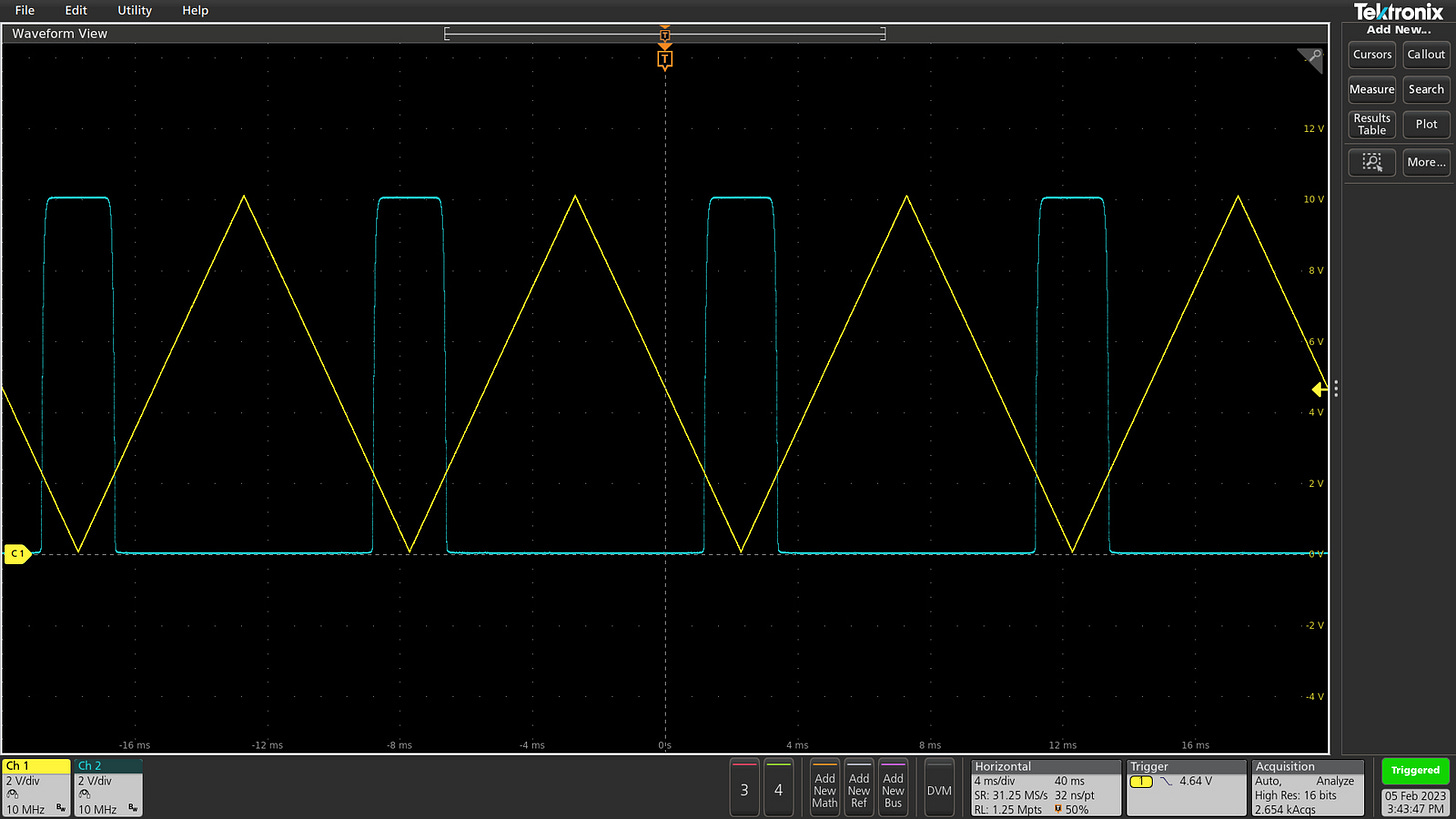
To analyze this circuit, let’s suppose that R = 10 kΩ, that the transistor’s threshold voltage is 2 V, and that a 5 V signal is supplied on the input terminal.
At first, the source terminal is at ground potential, so Vgs is equal 5 V and the transistor becomes conductive. Soon thereafter, in response to the flowing current, a voltage develops across the resistor (V = IR), dragging the source terminal to a higher potential. By the time the current reaches 300 µA, the source leg is at 3 V (10 kΩ * 300 µA), so Vgs is effectively reduced to 2 V. This is the threshold voltage of the transistor; any further increases in the current would cause it to shut off. We reach a equilibrium: Vout = Vsignal - Vth.
The following oscilloscope plot shows the behavior of the circuit; the input signal is shown in yellow, while the output is blue:
Of course, the circuit isn’t a voltage amplifier, but it is a building block for one. It does offer power gain if R is replaced with a real load, although its drive capabilities are asymmetric: if you connect a capacitor across its terminals, it will only be able to charge it to higher voltages as the input signal rises, not discharge it back when the input signal falls.
The oscilloscope plot shows a significant (Vth-related) offset between the input and the output signal; because the circuit can’t output voltages lower than the ground, some of the shifted waveform is also clipped. To avoid such distortion, one would need to gently offset the input signal beforehand.
Toward a voltage amplifier
Let’s make a small modification to the voltage follower circuit by adding a second resistor on the high side of the MOSFET:
For a moment, let’s assume that R1 = R2. The fundamental mechanism of the circuit remains the same: the transistor will admit current sufficient to create a self-limiting feedback voltage across R2. This voltage is always Vsignal - Vth. But because the same current is necessarily also flowing through the newly-added R1, the extra resistor will develop a voltage drop across its terminals that is identical to that seen across R2.
This may seem uninteresting, but now consider what happens if R1 is larger than R2. The current through the circuit would generally remain unchanged; and from V = IR, we know that if the current is constant and the resistance increases, we should see a proportionately larger voltage drop across R1.
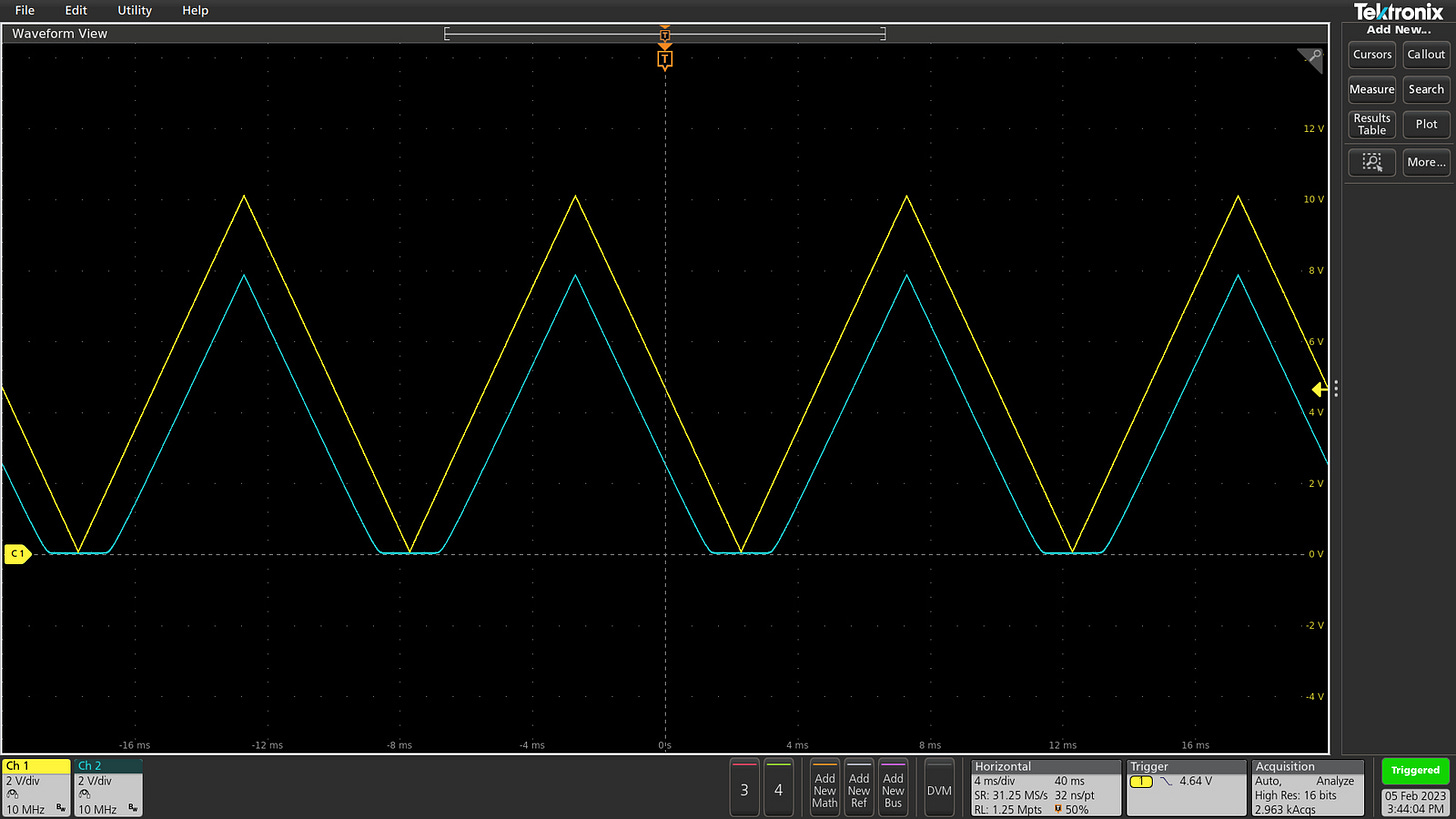
And indeed, we can observe this R1/R2 amplification behavior in the following oscilloscope trace produced for R1 = 100 kΩ and R2 = 10 kΩ. A weak input signal with a 400 mV amplitude (yellow) is producing a solid 4 V swing on the output (blue) — a nearly-perfect 10x boost:
Because R1 is dangling from the positive supply rail, the output is inverted: that is, low input voltages produce high output voltages (and vice versa). That minor inconvenience aside, the circuit is a solid amplifier with a well-defined and easily-adjusted gain.
The most significant issue with this circuit — and one glanced over by most online tutorials — is that the sum of voltage drops across the two resistors in series obviously can’t exceed the supply voltage. To understand the consequences, let’s go back once again to the unity gain configuration (R1 = R2). If the input signal is 8 V and the supply voltage is 10 V, you might be expecting a 6 V drop across R2 (8 V - Vth = 6 V), and then an identical drop across R1 that pulls the output -6 V from the positive rail. But of course, a total drop of 12 V is not attainable across two resistors connected in series between the terminals of a 10 V power supply. You will see 5 V at most.
The practical rule to remember is that in this amplifier circuit, Vout can’t drop below Vsignal - Vth. You lose about half the range at unity (1x) gain, but at higher amplification ratios, the loss is comparatively small.
Adding push-pull outputs
Their other warts aside, the circuits discussed so far are not suited for driving substantial loads: they either can’t source significant currents, or — in the case of a modified voltage follower — they do so asymmetrically, causing distortion with capacitive and inductive loads.
The solution is a push-pull power amplifier: a circuit that uses two complementary transistors — in this example, an n-channel and a p-channel MOSFET — to shuffle the load as appropriate across two supply rails:
This arrangement can be thought of as two conjoined voltage followers. The n-channel transistor pulls the output terminal toward the positive rail whenever Vout becomes too low (i.e., when Vsignal > Vout + Vth). The other transistor — p-channel — pushes the output toward the ground if it gets too high (i.e., Vsignal < Vout - Vth).
The transistors are never on at the same time, but because of their built-in threshold voltages, the circuit has a dead spot when both are turned off — an effect known known as crossover distortion:
With a floating output, the crossover voltage is poorly controlled, so the two Rload resistors (~10 kΩ) were added in the demo circuit to hold it steady during the transition.
The crossover can be largely eliminated by splitting the input signal into two branches and then individually offsetting each; this can be done with resistors, although diodes sometimes also make an appearance. The benefit of using a diode is that it maintains a fairly constant voltage drop across its terminals, whereas resistor-based dividers only provide outputs relative to supply voltage. Either way, once the gap is gone, the two Rload resistors can be safely removed.
Of course, by the time we’re done combining a voltage amplifier with a push-pull driver, and then offsetting all the voltages to eliminate Vth-related artifacts, we’re looking at about a dozen discrete parts. Surely, there has to be a simpler way?
Operational amplifiers
The answer is yes: let the fine folks at Texas Instruments do your job. Operational amplifiers are relatively simple integrated circuits that amplify the difference between two input voltages while maintaining very high input impedance, providing good current output capabilities, and keeping the signal distortion-free. Many modern op-amps are also capable of rail-to-rail inputs and outputs, further simplifying circuit design.
In other words, if you have an amplification problem that can’t be solved with 2-4 discrete components, an op-amp is probably the way to go.
In an open-loop configuration, a typical op-amp has a gain of 100,000 or more. It behaves essentially like a voltage comparator: if the voltage on the non-inverting (“+”) input is higher than on the inverting one (“-”), the output swings to somewhere near the upper rail. In the opposite situation, the output drops to the lowest possible voltage. There is a linear region in between, but it is poorly-defined and darn difficult to zero in on; as with transistors, adding some sort of a feedback mechanism is key.
Op-amp as a voltage follower
The simplest feedback-based op-amp circuit is a voltage follower, constructed by connecting the device’s output to its inverting input terminal.
To analyze this circuit’s behavior, let’s say that for whatever reason, the output pin momentarily ended up at a voltage lower than the signal provided on the non-inverting leg. This lower output voltage will be immediately reflected on the inverting input, creating a positive voltage differential across the input terminals. The op-amp will react by moving its output voltage higher until the balance is restored: Vin+ = Vin- = Vout. Strictly speaking, there will be some tiny difference between Vin- and Vin+, but only miniscule swings are needed to obtain the full range of Vout voltages — so the values are practically the same.
The opposite scenario, with Vout swinging too high, would unfold similarly and lead to a correction in the opposite way.
In most applications, there are no major gotchas with this design: as long as the input and output voltages are staying with the spec, there should be no substantial offset, distortion, or input impedance surprises. Much like digital ICs, op-amps are designed to abstract away much of the underlying transistor-related ickiness.
A non-inverting voltage amplifier
A simple modification of the previous circuit is to add a resistor-based voltage divider on the feedback loop:
Suppose that R1 = R2; it should be clear that the voltage presented on the Vin- leg will be equal to one half of Vout. It follows that to reach equilibrium on its differential inputs, the op-amp needs to output twice the voltage supplied on the non-inverting leg. In effect, we have a 2x voltage amplifier. Increasing R1 will further increase gain; the formula is 1 + R1/R2.
In practice, it is common to see R2 values around 10 kΩ, and R1 perhaps all the way into megaohms. High resistances usually don’t hurt, although they might reduce bandwidth or increase noise; some experimentation is advised.
Inverting amplifiers
A variation of the basic op-amp topology combines the input voltage and the feedback signal on the same inverting leg:
To analyze the behavior of this circuit, let’s once again assume that R1 and R2 are identical. If the input signal is disconnected, the circuit acts as a voltage follower; given the op-amp’s huge input impedance, the feedback current is negligible, so R1 is not having much of an effect.
If we reconnect the input signal, the situation changes a bit: Vin- is now seeing a 50-50 mix of Vsignal and Vout. If a 100 mV spike arrives from the signal source, it will push the inverting input up by 50 mV. When that happens, the inverting leg is all of sudden more positive, to the amplifier starts reducing its output voltage until Vin- = Vin+. To compensate for the 50 mV increase on Vin-, Vout would have to drop by 100 mV.
In effect, with R1 = R2, we have an inverting voltage follower; if R1 is increased, the circuit becomes a voltage amplifier with a gain of -R1/R2.
The advantage of this circuit topology is that the reference point for amplification is determined by Vref, so we can remove or add DC biases without mucking with the input signal directly. On the flip side, the input impedance of an inverting amplifier is a bit lower, due to the feedback resistor connecting Vin- and Vout.
Op-amp frequency considerations
Most general-purpose IC-based amplifiers have a deliberately limited bandwidth: a built-in lowpass filter causes the maximum attainable gain to decrease as the frequency of the input signal goes up, eventually causing the op-amp to stop amplifying once the gain drops below 1x.
Although real op-amps can't have infinite bandwidth either way, the reason why they have a carefully limited frequency response is that the amplifier inevitably exhibits some parasitic capacitance. The capacitance creates an apparent sine-wave lag between input and output signals — and thus, a delay in the feedback signal used to control gain. As the signal frequency increases, the phase delay grows, and the feedback signal has less and less to do with reality. Without lowpass filtering, the eventual consequence is excessive amplification, ringing, or even sustained oscillations once the phase shift approaches one half of the wavelength.
Because of the built-in bandwidth limitations, the datasheet for every op-amp will specify either “unity-gain bandwidth” or “gain-bandwidth product” (GBP). For normal (“fully-compensated”) amplifiers, the values should be the same thing. When dealing with op-amps configured to amplify voltages, you can take the number and divide it by the voltage gain you’re hoping to achieve; the result will be the maximum frequency you can pass through without substantial loss.
As a practical example, let’s say I want to use the TLV4110 op-amp to amplify some audio signal by a factor of 200. The IC has unity-gain bandwidth of 2.7 MHz; at my intended gain, the amplifier should hold up reasonably well to 13.5 kHz (2.7 MHz / 200). While not great, it should be enough to handle medium-definition sound.
Another frequency-related characteristic of op-amps is their slew rate — that is, the speed with which they can swing their output from one rail to another. For example, the TLV4110 has a slew rate of 1.5 V/µs; if operated at 10 V, swinging from one rail to another and back would take ~13.3 µs. This understandably limits the ability to amplify large signals at high speed.
As for discrete transistors, the main limiting factor for larger MOSFETs is their gate capacitance: they essentially behave like capacitors that need to be charged or discharged every time you’re changing their gate voltage. For low-power (“signal”) transistors, the capacitance is a couple picofarads; for larger ones, it might be well into the nanofarad range. It follows that power MOSFETs can’t be driven directly by an MCU at higher speeds; problems begin to mount in the kilohertz range. A small transistor- or op-amp preamplifier can help. In any circuit that uses feedback, potential phase lag should be taken into consideration, too.
Amplifier noise considerations
Signal amplification and noise go hand in hand, but a detailed discussion of this topic would make an already-overlong article even harder to digest. In lieu of a deep dive, here are some troubleshooting tips for noisy amplifiers:
Keep any resistance in series with weak signals as low as practical to minimize Johnson–Nyquist noise. If you’re running into op-amp issues, lowering the value of feedback resistors might also help.
Use lowpass or bandpass filters to avoid amplifying stray RF signals picked up by your circuit. Through several different mechanisms, high-frequency signals can sometimes turn into audible squeals or hiss.
Keep all signal wiring short. If you need to run it some distance, use twisted pair or coax.
Use low-ESR decoupling capacitors around high-speed digital circuitry that is a part of the same device — and keep the digital bits at an arm’s length on the PCB. If in doubt, sprinkle 100 nF MLCC capacitors generously across the PCB.
Use ferrite beads or small resistors on high-speed data busses and on the voltage supply lines ahead of digital circuitry section whenever practical; these can control inrush currents and reduce voltage spikes and EMI.
Make sure you have a good, low-impedance ground path that is uninterrupted and physically close to any high-speed signal lines. This will limit stray electric and magnetic fields. A fully-fledged ground plane or metal shielding can limit some types of RF issues, too.
Don’t use trashy power supplies. That includes no-name USB wall warts. As a last resort, batteries will always provide cleaner power than a switching power supply.
If you liked this article, please subscribe! Unlike most other social media, Substack is not a walled garden and not an addictive doomscrolling experience. It’s just a way to stay in touch with the writers you like.
For a follow-up article dealing with the inner workings of op-amps and current sources, click here. For a practical microphone amplifier circuit, read this article. More on op-amp instability can be found here. To review the entire series on electronics, check out this page.