Algorithms & math trivia
A fairly common theme on this blog are write-ups about computer algorithms and mathematical curiosities. Although these are covered in countless other placed on the internet, I think the following articles go above and beyond. They don’t just recite formulas; they explain the “why” in ways that should make sense to folks without a PhD.
Note that the page omits some articles that focus on programming trivia (example); for a complete list, you can refer here.
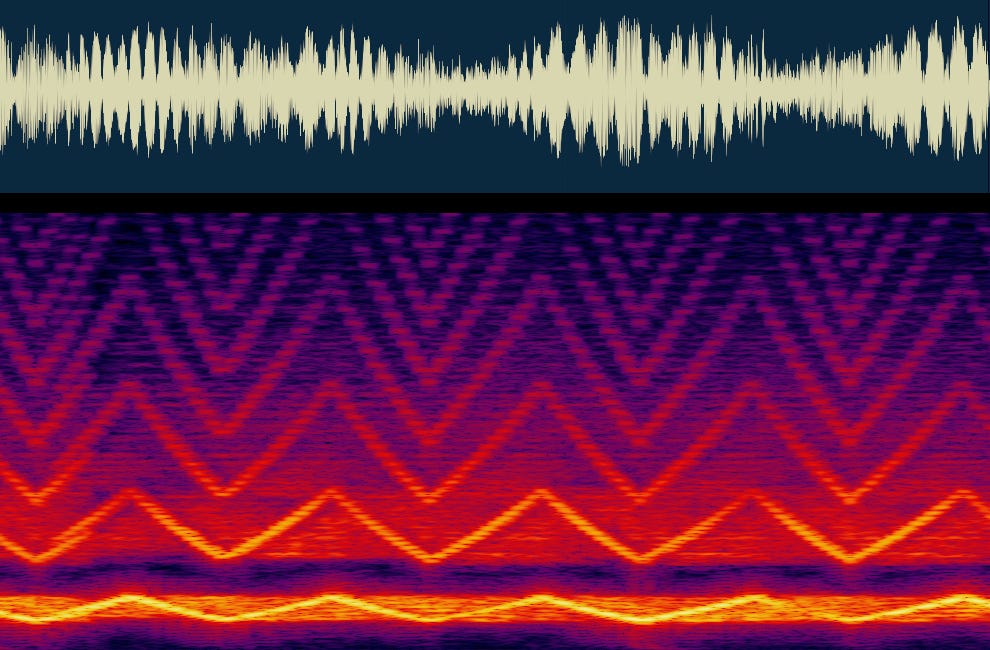
Not so fast, Mr. Fourier!
The discrete Fourier transform (DFT) is one of the most important algorithms in modern computing: it plays a key role in communications, image and audio processing, machine learning, data compression, and much more. Curiously, it’s also among the worst-explained topics in computer science. Let's have a closer look.
Is the frequency domain a real place?
In the earlier article on the Fourier transform, I talked about the frequency domain — a wondrous mathematical place where complex signals are transmuted into the amplitudes and phases of sine waveforms. But how real is this place, anyway, and does the DFT hold a monopoly on truth?
A 20-minute intro to complex numbers
Complex numbers are a fairly abstract construct that reeks of higher math, but they crop in software engineering, electronics, and beyond. Their basic structure is explained in many places on the internet; what's less clear is why they're constructed this particular way.
Complex numbers #2: a world in 3D
In the previous article, I talked about complex numbers. Can we extend that concept to three dimensions? Yes, sort of: with quaternions. Once again, the concept is explained elsewhere on the internet, but this article goes beyond the formulas and addresses the "how".
0.9999... ≊ 1
I’ve been long fascinated by the endless online debates about whether the infinite decimal expansion 0.9999… is exactly equal to 1. The canonical answer is yes - but it's actually hard to properly substantiate that claim!
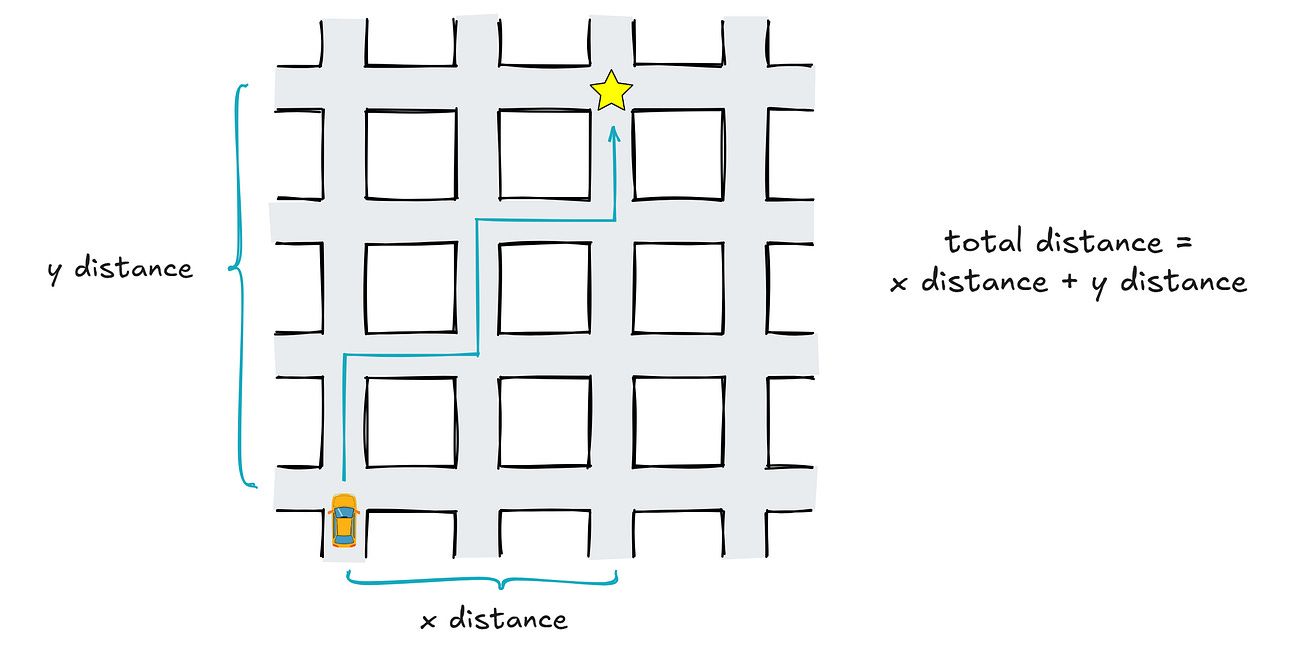
π = 4
In the earlier article, I discussed the perils of thinking about infinity as a number. In this followup, we have a look at a peculiar infinity-related "proof" that π = 4. The proof is less wrong than it may seem!
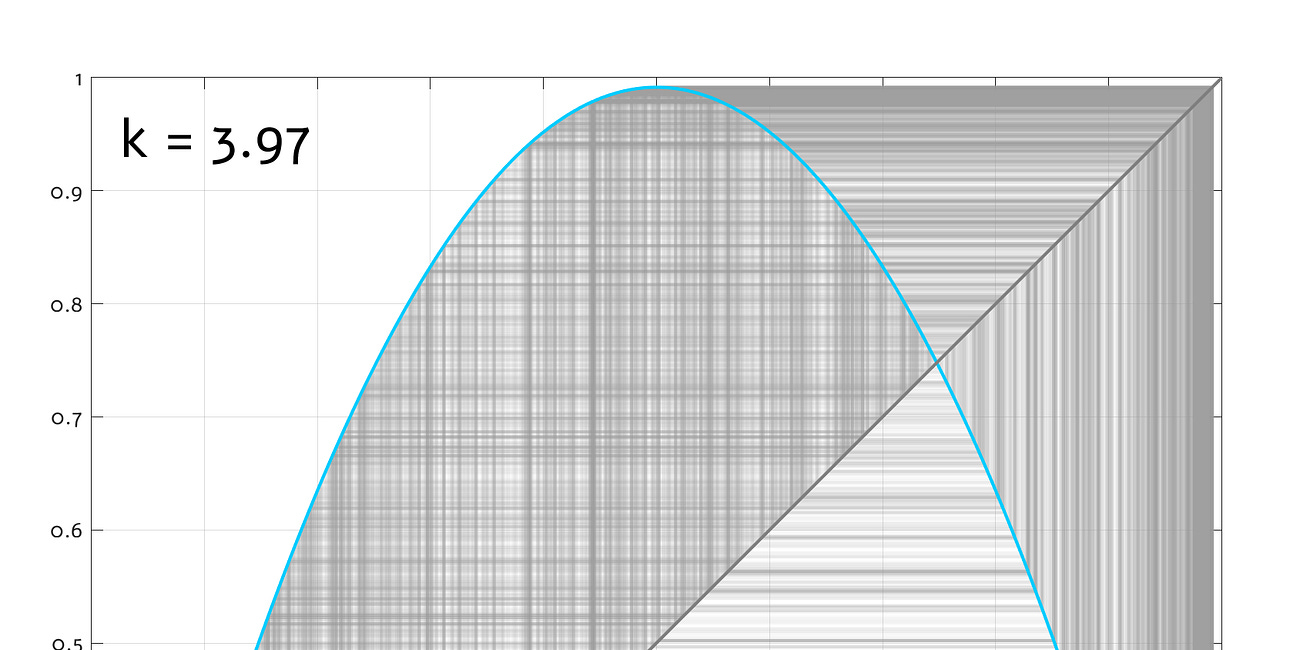
Fractals #2: understanding Mandelbrot
Almost every computer nerd knows the Mandelbrot fractal. But where does its complex 2D structure really come from?
Sierpiński triangle? In my bitwise AND?
An unexpected visitor: how come a familiar fractal crops up when you count in binary?
If you have suggestions or other feedback, you can reach me at lcamtuf@coredump.cx.